The joint influence of break and noise variance on the break detection capability in time series homogenization

Instrumental climate records of the last centuries suffer from multiple breaks due to relocations and changes in measurement techniques. These breaks are detected by relative homogenization algorithms using the difference time series between a candidate and a reference. Modern multiple changepoint methods use a decomposition approach where the segmentation explaining most variance defines the breakpoints, while a stop criterion restricts the number of breaks. In this study a pairwise multiple breakpoint algorithm consisting of these two components is tested with simulated data for a range of signal-to-noise ratios (SNRs) found in monthly temperature station datasets. The results for low SNRs obtained by this algorithm do not differ much from random segmentations; simply increasing the stop criterion to reduce the number of breaks is shown to not be helpful. This can be understood by considering that, in case of multiple breakpoints, even a random segmentation can explain about half of the break variance. We derive analytical equations for the explained noise and break variance for random and optimal segmentations. From these we conclude that reliable break detection at low but realistic SNRs needs a new approach. The problem is relevant because the uncertainty of the trends of individual stations is shown to be climatologically significant also for these small SNRs. An important side result is a new method to determine the break variance and the number of breaks in a difference time series by studying the explained variance for random break positions. We further discuss the changes from monthly to annual scale which increase the SNR by more than a factor of 3.

1 Introduction

Relocations of climate stations or changes in measurement techniques and procedures are known to cause breaks in climate records. Such breaks occur at a frequency of about one per 15 to 20 years and the break sizes are assumed to follow a normal distribution (Menne and Williams Jr., 2005) with a standard deviation of about 0.8 K (Auer et al., 2007; Menne et al., 2009; Brunetti et al., 2006; Caussinus and Mestre, 2004; Della Marta et al., 2004; Venema et al., 2012). It is obvious that a few of such breaks have the potential to introduce large errors into the station temperature trends observed during the last century.

Numerous homogenization algorithms exist aiming to detect and correct these breaks. Benchmarking studies (Venema et al., 2012; Williams et al., 2012) analyze the quality of homogenized datasets and as such they consider whole homogenization algorithms, whereas in this study we concentrate on the detection only. The overall performance is investigated by simulated data that model as accurately as possible both the natural variability and the statistical properties of the hidden breaks. Venema et al. (2012) presented the results of the COST Action HOME, which tested the skills of the most commonly used methods and state-of-the-art algorithms by a prescribed fixed assessment procedure. Nearly all of them were relative methods that use the difference either to a composite reference or to a neighboring station to reduce the natural variability that otherwise would conceal the breaks.

The concrete implementation of the various methods differs, but the principal design of the methods is similar and comprises either two or three steps. The first step is the detection of breaks. Here, the difference time series is decomposed into subsegments with maximally different means. For pairwise methods, an intermediate step, the so-called attribution, follows, where detected breaks of the difference time series are assigned to one of the involved stations. Finally, the break sizes for each station and break are determined by a comparison with the neighbors. Although a simultaneous correction of all breaks is more accurate (Domonkos et al., 2013), most algorithms analyzed by Venema et al. (2012) correct break by break beginning today and moving backward in time, such as PHA (Menne et al., 2009), iCraddock, (Craddock, 1979; Brunetti et al., 2006), AnClim (Štépanek et al., 2009), and the various SNHT variants (Alexandersson and Moberg, 1997) that participated.

HOME recommended five homogenization methods: ACMANT (Domonkos, 2011), PRODIGE (Caussinus and Mestre, 2004), MASH (Szentimrey, 2007, 2008), PHA, and Craddock. These methods have in common that they have been designed to take the inhomogeneity of the reference into account, either by using a pairwise approach (PRODIGE, PHA, Craddock) or by carefully selecting the series for the composite reference (ACMANT, MASH). Furthermore, most of these methods explicitly use a multiple breakpoint approach (ACMANT, PRODIGE, MASH).

As mentioned above, we focus in this study on the break detection of such modern multiple breakpoint methods (Caussinus and Mestre, 2004; Hawkins, 2001; Lu et al., 2010; Picard et al., 2005, 2011). While Lindau and Venema (2016) concentrated on the errors in the positions of the breaks, here we analyze the deviation of the estimated inhomogeneity signal from the true one. We consider the difference time series between two neighboring stations as raw information consisting of two components: the break and the noise series. The climate signal is cancelled out, because it is assumed to be the signal both stations have in common, whereas any local deviation from the climate is treated as noise. The main task of homogenization algorithms is to filter out the break part, which can be considered as a signal. Obviously, the task becomes more difficult for low signal-to-noise ratios (SNRs).

The number of breaks is normally determined by considering the likelihood of falsely detecting a break in white noise (Lindau and Venema, 2013). The key idea of this paper is that both the break and noise variance need to be considered. We will show that about half of the break variance is explainable even by random break positions. If the noise is large, the total maximum variance is often attained when the break positions are set in a way that most of the noise is explained. The large amount of additionally (but just randomly) explained break variance suggests erroneously that significant breaks have been found. The algorithm correctly detects that the series contains inhomogeneities, but the errors in the positions can be large. In this paper, we use a basic detection algorithm, consisting only of the two main components: optimal segmentation and a stop criterion. We test the performance of this multiple breakpoint algorithm concerning the detection and its ability to stop the search using simulated data with the same SNR as is typically found in observed temperature data.

The paper is structured in the following way. Section 2 presents the used observations, their processing, and the method to determine the best neighbor in order to build pairs for the difference time series. In Sect. 3 we show that breaks in climate series are indeed a relevant problem in the real world or at least for the analyzed German climate stations. Section 4 describes the applied break search method. In Sect. 5 we distinguish between break and noise variance, and derive four formulae, which describe the behavior of both variance parts (noise and breaks) for two scenarios: for optimum and arbitrary segmentations. These findings are used in Sect. 6 to estimate the range of SNRs found in real data. In Sect. 7 we use this range and derive theoretically why we expect that the break search method must fail for low SNRs. In Sect. 8 we generate simulated data with realistic SNRs to follow the process of finding the optimum segmentation. A skill measure to assess the quality of segmentation is presented. For realistic SNRs of 1∕2, it shows that random segmentations attain the same skill as the search method used here. Section 9 concludes this study.

2 The observations and the method to build pairs

This study consists mainly of general considerations about the segmentation approach used in homogenization algorithms. Mostly, we will confirm our findings by simulated data with known statistical properties. However, in order to use the correct settings for these properties, we also analyze real observations.

For this purpose, we use data from German climate stations (Kaspar et al., 2013) provided by the DWD (Deutscher Wetterdienst), which report the classical weather parameters, e.g., air temperature, air pressure, and humidity, three times a day. These data are aggregated to monthly resolution. The analysis is restricted to the period 1951 to 2000. This period is expected to have relatively few inhomogeneities and has a high station density. Before 1951, the spatial data density was much lower and nowadays many stations are closing due to funding cuts. In this way, our database comprises 1050 stations with 297 705 average monthly temperature observations in total.

First, normalized monthly anomalies are calculated for each station by subtracting the mean and dividing by the standard deviation of the monthly mean temperature (both for the period 1961 to 1990). In this way the variability of the annual cycle is almost completely removed, which would otherwise dominate. Using the obtained normalized anomalies we build the difference time series against the best neighbor station, which needs to be within a range of 100 km and have at least 200 overlapping monthly observations. As mentioned above, difference time series are necessary to cancel out the large natural variability, which would otherwise dominate. We use two criteria to select the best neighbor j₀(i) for a given station i from all its neighbors $j=\mathrm{1},\mathrm{\dots },j_{\mathrm{all}}$: the fraction of overlapping data coverage f(i,j) and the correlation r(i,j) between the two time series, which determines the variance of the difference time series.

$$\begin{array}{}\text{(1)}& {\displaystyle }{j}_{\mathrm{0}}\left(i\right)=\underset{\mathrm{1}\le j\le j_{\mathrm{all}}}{\mathrm{argmin}}\left({\displaystyle \frac{\mathrm{1}-r(i,j)}{f(i,j)}}\right),i\ne j\end{array}$$

3 Estimation of the trend errors due to breaks in real data

Providing reliable secular trends of meteorological parameters is one of the major tasks in climatology (Lindau, 2006). In the following we analyze the DWD station data to show that there are actually problems in determining the long-term temperature trend, which are obviously caused by inhomogeneities. So this section can be seen as motivation that homogenization does actually matter. Trends are calculated using linear least squares regression. To make it easier to appraise the climatological relevance of the trends, the anomalies are not normalized by the standard deviation when computing trends.

We start with calculating the trends of the difference time series between two neighboring stations. In case of trends we increase the requirements and take only pairs into account with a fully covered baseline period 1961 to 1990. This reduces the database to 171 642 observations at 316 station pairs.

It is important that the difference between two neighboring stations is considered here. Due to their proximity the climate signal is expected to be similar at both stations and is nearly entirely cancelled out in the difference time series. Therefore, usually we can assume that the difference series consists of noise plus inhomogeneities, so that we can attribute any significant deviation of the trend from zero and any serial correlation of the difference data to the inhomogeneities. This assumption is the basis for relative homogeneity tests. If the assumption that the climate signal is largely cancelled out does not hold true, any true trend remaining in the difference time series will be treated as a gradual inhomogeneity which will then be corrected by mistake. Thus, significant trends in the difference time series of neighboring stations indicate either the presence of inhomogeneities or large problems in applying relative homogenization at all. For Germany the former is likely the case.

Figure 1 shows the difference time series of monthly temperature anomalies between Aachen and Essen for the period 1950 to 2000. The 2-year running mean shows a distinct deviation from zero in the late 1970s, which already provides some indication of an inhomogeneity. The most striking feature, however, is the strong linear trend of 0.564 K per century, which is not expected for homogeneous difference time series. Assuming independence, i.e., no inhomogeneities, the standard error in the trend estimation is as low as 0.074 K century⁻¹, indicating an apparently high significance of the difference trend itself. This contradicts the assumption that trends of difference time series should not differ significantly from zero.

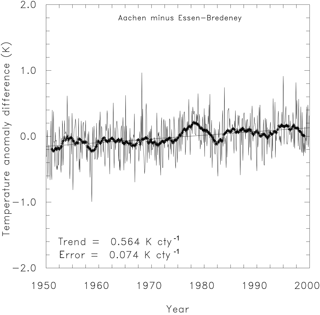
Figure 1 Difference time series of the monthly temperature anomaly between stations Aachen and Essen. The two stations are separated by 92 km and their correlation coefficient for monthly means is 0.989. The thick line denotes the 2-year running mean; the thin line is the linear trend. The error variance of the trend assuming (probably erroneously) independent data is calculated by ${\mathit{\sigma }}_{\mathrm{trend}}^{\mathrm{2}}=\frac{{\mathit{\sigma }}_y^{\mathrm{2}}\left(\mathrm{1}-r^{\mathrm{2}}\right)}{{\mathit{\sigma }}_x^{\mathrm{2}}\left(n-\mathrm{2}\right)}$ for data on the y axis and time on the x axis, while r denotes the correlation between data and time and n the length.

We repeated the procedure for 316 station pairs in Germany (Fig. 2). The short vertical lines give the (much too low) uncertainty assuming temporal independence of data. The horizontal line in the middle denotes the mean over all stations. The upper and lower lines show the actually obtained standard deviation of all station pair trends. The mean trend is near zero, as expected for differences. The sign is not relevant here, as simply exchanging the order within the pairs would reverse it. The interesting feature is the standard deviation of the difference trends, representing the true uncertainty of the trends. Averaged over all the station pairs in the German climate network, the trend in the difference series is 0.628 K century⁻¹, which indicates that the example shown in Fig. 1 (with 0.564 K century⁻¹) is not the exception, but a common situation.

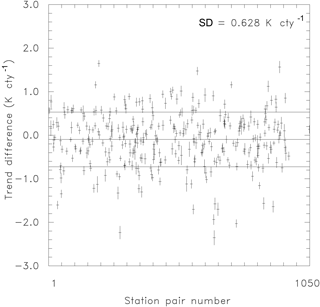
Figure 2 Trends for the difference time series of 316 station pairs (from 1050 stations) in Germany. The standard deviation is 0.628 K per century, much higher than expected for homogenous independent data (short vertical lines).

As two stations could be contributing to the inhomogeneities, the standard deviation contributed by one station equals the standard deviation of the difference series divided by the square root of 2. Thus, the trend error caused by inhomogeneities in one station data series is about 0.4 K century⁻¹ (i.e., 0.564 K century⁻¹ divided by the square root of 2), which is comparable to the observed global temperature change itself of about 1 K century⁻¹ (Hartmann et al., 2013). This trend error estimation assumes that the average break size is equal to zero. The possible impact of a network-wide non-zero break bias is not included (i.e., when the inhomogeneities produce on average a non-zero trend), since this overall effect vanishes for trend differences.

4 The break search method used

In order to identify the obviously existing inhomogeneities, we use the following break search method. We split the considered difference time series (of length n) into k+1 segments by inserting k test breaks at random positions (not necessarily coinciding with the true unknown break positions) and check the explained variance of this segmentation. Since the test break positions are random, the lengths of the test segments vary and are given by l_i, $i=\mathrm{1},\mathrm{\dots },k+\mathrm{1}$. Observations are denoted by x_ij, where $i=\mathrm{1},\mathrm{\dots },k+$1 indicates the segment and $j=\mathrm{1},\mathrm{\dots },l_i$ the individual elements within the segment. We define two kinds of averages: $\overline{x}$ is the mean over the entire length of the series n and $\overline{x_i}$ is the mean of a specific test segment i within the time series. The total variance of a time series (diminished by the error variance of the total mean) is then equal to the sum of the external variance between the segment means and the internal variance within the segments (Lindau, 2003):

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^{k+\mathrm{1}}\sum _{j=\mathrm{1}}^{l_i}{\left(x_{ij}-\overline{x}\right)}^{\mathrm{2}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^{k+\mathrm{1}}{l}_i{\left(\overline{x_i}-\overline{x}\right)}^{\mathrm{2}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^{k+\mathrm{1}}\sum _{j=\mathrm{1}}^{l_i}{\left(x_{ij}-\overline{x_i}\right)}^{\mathrm{2}}.\end{array}$$

Normalized variances are obtained by dividing Eq. (2) by the total variance:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\sum _{i=\mathrm{1}}^{k+\mathrm{1}}{l}_i{\left(\overline{x_i}-\overline{x}\right)}^{\mathrm{2}}}{\sum _{i=\mathrm{1}}^{k+\mathrm{1}}\sum _{j=\mathrm{1}}^{l_i}{\left(x_{ij}-\overline{x}\right)}^{\mathrm{2}}}}+{\displaystyle \frac{\sum _{i=\mathrm{1}}^{k+\mathrm{1}}\sum _{j=\mathrm{1}}^{l_i}{\left(x_{ij}-\overline{x_i}\right)}^{\mathrm{2}}}{\sum _{i=\mathrm{1}}^{k+\mathrm{1}}\sum _{j=\mathrm{1}}^{l_i}{\left(x_{ij}-\overline{x}\right)}^{\mathrm{2}}}}=V+v=\mathrm{1},\end{array}$$

where V denotes the normalized external, and v the normalized internal, variance. Furthermore, V can be interpreted as that fraction of variance which is explained by the chosen segmentation. The decomposition into internal and external variance is applied in the state-of-the-art break search algorithms, such as PRODIGE (Caussinus and Mestre, 2004) and ACMANT (Domonkos, 2011), which both use the maximum external variance V_max(k) as a break criterion that determines the true break positions. V_max(k) is defined as the maximum variance attainable by any combination of break positions for a given number of breaks k. This optimum segmentation containing the maximum external variance V_max is determined by using the optimal partitioning approach (Bellman, 1954; Jackson et al., 2005) separately for each number of breaks k. In this approach, the multiple re-use of solutions from truncated sub-series speeds up the search drastically (compared to a test of all combinations), which is described in more detail in Lindau and Venema (2013). The algorithm searches for an optimum segmentation using minimum unexplained variance as a criterion. The method works because the unexplained variance of any segment can be obtained by the weighted sum of the variance of two arbitrary subsegments. Based on this additive property the idea of optimal partitioning is the following: the optimal solution for k breaks is derived for not only full-length series, but also for all truncated sub-series. In this way the minimum variance for k+1 breaks can be obtained by the sum of two variances: that of the truncated series for k breaks plus that of the rest series for zero breaks.

However, the maximum external variance V_max grows with each additionally assumed break, reaching full variance if n−1 breaks were tested within a time series of length n. Such a useless continuation of inserting more and more test breaks is prevented by the stop criterion, which limits the numbers of breaks by a penalty term for each additional break. Following Caussinus and Lyazrhi (1997), we use

$$\begin{array}{}\text{(4)}& {\displaystyle }{n}_k=\underset{\mathrm{0}\le k<n}{\mathrm{argmin}}\left(\ln \left(\mathrm{1}-V_{max}\left(k\right)\right)+{\displaystyle \frac{\mathrm{2}k\ln \left(n\right)}{n-\mathrm{1}}}\right).\end{array}$$

By Eq. (4) the true number of breaks n_k is determined as that number which minimizes the logarithm of the normalized internal variance plus a penalty term, where the penalty term is a linear function of k with a growth rate depending on the total length n. Thus, the break search algorithm used in this study consists of two steps. (1) Searching for the segmentation containing the maximum external variance V_max for each break number k. (2) From the found candidates of V_max(k) the final solution is determined by applying the stop criterion given in Eq. (4). The name “stop criterion” is commonly used, but could be misleading, because it may suggest that the search is actually stopped at a certain number of breaks. However, the definition given in Eq. (4) makes it clear that we do not stop the search literally at a certain number of breaks. Instead we calculate the value of the expression given in Eq. (4) for all reasonable numbers of breaks k and determine the minimum of these candidates afterwards, which is then considered the optimal solution.

5 Break and noise variance

The difference time series of a climate station pair can be regarded as two superimposed signals. Firstly, the pure break signal, modeled as a step function. Secondly, a short-term variance produced by weather variability and random observations errors, which both lead to random differences between the stations. The break signal is the signal to be detected. Assuming it to be a step function is a good approximation even in case of gradual inhomogeneities, which in the presence of noise can be modeled well by several steps; see the PRODIGE contributions in Venema et al. (2012). The noise stems from measurement errors and differences in the local weather. The weather noise can be autocorrelated, for example in regions influenced by El Niño, but in most cases these correlations are low and do not influence the result much. The HOME benchmarking study used both independent and autocorrelated simulated data and the autocorrelated data were more difficult to homogenize, but not much. For simplicity we thus apply the common assumption that the noise is independent. For both break and noise part we will give formulae that describe the external variance (i.e., explained by the segmentation). This is done twice, for random and optimum segmentations, so that we will finally obtain four formulae.

5.1 Noise variance

Lindau and Venema (2013) discussed the noise part of the variance in detail. Assuming Gaussian white noise with the variance ${\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}$, they found that for random test breaks the external variance part grows linearly with the number of the tested breaks k:

$$\begin{array}{}\text{(5)}& {\displaystyle }{V}_{\mathrm{Nave}}\left(k\right)={\displaystyle \frac{k}{n-\mathrm{1}}}{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}},\end{array}$$

where n denotes the total length, ${\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}$ the total noise variance, and V_Nave(k) the explained variance averaged over all possible combinations, assuming k breaks (Fig. 3, lower curve). If as many breaks as possible are assumed (i.e., $k=n-\mathrm{1})$, the entire variance ${\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}$ is explained. Equation (5) states that the variance gain with increased test break number k is linear. However, this is only valid on average. If k breaks are inserted randomly into a time series of length n, there are $\left(\begin{array}{c}n-\mathrm{1}\\ k\end{array}\right)$, and thus a huge number of possible combinations. The linear relation of Eq. (5) is obtained only if we average over all these possibilities for a given number of k. Therefore, we can call V_Nave the average behavior for noise, or alternatively, the expected value of explained variance for randomly inserted test breaks into noise data.

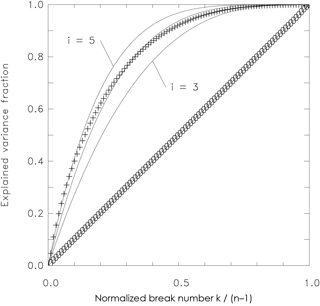
Figure 3 External variance as a function of the tested number of breaks for random (0) and optimum segmentations (+). The latter can be approximated by Eq. (6): auxiliary lines for exponents of 3, 4, and 5 are given additionally.

However, in break search algorithms the optimum segmentation (e.g., derived by optimal partitioning) is relevant rather than the mean behavior. It is obvious that the best of a huge number of segmentations is able to explain more than an average or random segmentation. Lindau and Venema (2013) found that the external variance of the optimum segmentation grows with k by

$$\begin{array}{}\text{(6)}& {\displaystyle }{V}_{\mathrm{Nmax}}\left(k\right)=\left(\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{k}{n-\mathrm{1}}}\right)}^i\right){\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}},i\approx \mathrm{5}.\end{array}$$

Equation (6) is an approximation; the exponent i is not completely constant for all k. To assess the change in the exponent, we added three auxiliary lines (Fig. 3, upper curve), giving Eq. (6) for i=3 to 5 to estimate the exponent for the shown simulated data. For small k, the exponent is equal to about 5, decreasing gradually to 4 when the normalized break number $k/\left(n-\mathrm{1}\right)$ approaches 0.5. However, a realistic break number is small compared to n, so that an exponent of 5 is in most cases a good approximation.

5.2 Break variance

So far we have discussed the behavior of the noise part of the time series. The next important question is how the signal or break part behaves. For pure breaks without noise we assume a step function with a constant value between two adjacent breaks (Fig. 4). Tested segment averages are the weighted means of such (few) constant periods. This is a similar situation to random noise, only that fewer independent data are underlying. Obviously, the number of breaks n_k now plays a similar role to what the time series length n did before for random noise. Consequently, we expect the same mathematical behavior, but on another scale, because n_k is normally much smaller than n.

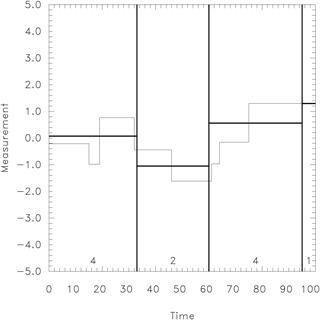
Figure 4 An example of a noise-free time series containing seven true breaks (thin step line) is tested with three random breaks denoted by the thick vertical lines. The resulting averages for each test segment are given by thick horizontal lines. Their variation defines the explained variance. At the bottom of each test segment the number of independent values is given. The total number of independents is equal to 11, or, more generally, $n_k+\mathrm{1}+k$.

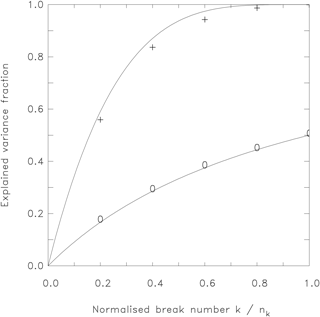
Figure 5 Empirical estimates of the external variance as a function of the normalized number of tested breaks for random (0) and optimum (+) segmentations. Analytical functions (Eqs. 7 and 8) are given for comparison, similar to Fig. 3, but for a pure break signal and with a different normalization. The empirical estimates are based on 1000 simulated time series of length 100 with five breaks at random positions.

To check our assumption, we used simulated data of length n=100 including n_k=5 breaks without any noise (Fig. 5). A length of 100 is assumed, because homogenization is often applied to yearly series to reduce the noise and to reduce the serial correlation, which might remain in serial monthly series; 100 years is the typical length of such a climate record. If monthly data are analyzed, the series of all Januaries or Julies is often considered separately, which results in the same length. We distinguish between the true break number n_k (which is normally unknown) and the tested break number k running from 1 to n−1 during the break search. As expected, the best segmentations for pure breaks (Fig. 5, upper curve) behave similarly to the best segmentation for pure noise (compare Fig. 3, upper curve). However, an important difference is that the tested break number k is now normalized by the true break number n_k instead of n−1. Hereby the external break variance grows (with increasing k) much faster than the external noise variance, because n_k≪n. This is the main reason why the discrimination of noise and signal and thus the break detection is possible at all. For the best segmentations of the break variance ${\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}$, we can write

$$\begin{array}{}\text{(7)}& {\displaystyle }{V}_{\mathrm{Bmax}}\left(k\right)=\left(\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{k}{n_k}}\right)}^i\right){\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}},i\approx \mathrm{4}.\end{array}$$

Please note that the explained variance given in Eq. (7) depends on the relation between used break number k and true break number n_k. Thus Eq. (7) does not depend on the total length of the time series n. This characteristic becomes plausible by referring to Fig. 4. There is no substantial change when the resolution on the x axis is increased from, e.g., 100 to 1000 time points. We still consider a step function (giving the true breaks) transected by a number of test breaks.

A further difference occurs for the random segmentations of the break signal. Please compare the two lower curves in Figs. 3 and 5. In contrast to the formula found for the noise part V_Nave (Eq. 5), V_Bave does not grow linearly with k, but with

$$\begin{array}{}\text{(8)}& {\displaystyle }{V}_{\mathrm{Bave}}\left(k\right)={\displaystyle \frac{k}{n_k+k}}{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}.\end{array}$$

The results of the simulations are given as crosses and circles in Fig. 5, confirming the validity of Eqs. (7) and (8) that both are given as curves for comparison.

In the following we provide an interpretation of Eq. (8) and an explanation why it differs from Eq. (5). We start with Eq. (5), which states that in case of pure noise the external variance decreases with increasing n. This becomes plausible when we consider the definition of the external variance: it is equal to the variance of the segment means (compare Eq. 2, first right-hand side term). The more independent values are underlying, the less the means vary, and the smaller the external variance is. Therefore, it is justified to interpret the variable n in Eq. (5) as the number of independent values in each segment summed over all segments.

Let us now use this finding to interpret Eq. (8). In a time series containing only breaks and no noise, there are originally n_k+1 independent values as illustrated in Fig. 4 by the constant thin-lined segments. In the example shown it contains seven true breaks (i.e., eight independents). A randomly tested combination of break positions is sketched by thick vertical lines, here with k=3. Each tested break (if it does not coincide accidentally with a true break) cuts a true segment into two pieces. These then contribute to two different tested subperiods. In this way, the effective number of independents is increased from n_k+1 to $n_k+\mathrm{1}+k$. Consequently, n−1 (the number of independents minus 1 for noise), appearing in the denominator of Eq. (5), has to be replaced by n_k+k (the number of independents minus 1 for breaks) to approximate the behavior for true breaks (Eq. 8).

With Eqs. (5) to (8), we are able to describe the growth of four types of external variance as a function of the tested break number k. We distinguish noise (Eqs. 5 and 6) and break variance (Eqs. 7 and 8), for both random (Eqs. 5 and 8) and optimum (Eqs. 6 and 7) segmentations.

6 Estimation of the break variance

The break variance ${\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}$ and the true break number n_k are important parameters to assess the quality of a climate record. If the SNR is high enough they can be estimated after applying a full homogenization algorithm, but even in that case such an estimate would be biased, since not all breaks are large enough to be detectable. However, our findings in Sect. 5 about the different reactions of true breaks (Eq. 8) and noise (Eq. 5) on randomly inserted test breaks make it possible to estimate the break variance and the break number in advance from the raw data.

We take an observed difference time series and test how much variance is explained by randomly inserted breaks. This is performed by calculating the external variance V(k). Since we test for random break positions, V_Nave and V_Bave from Eqs. (5) and (8) has to be applied to describe to theoretical expectation of this experiment. Thus, we expect a fraction of $k/\left(n-\mathrm{1}\right)$ of the noise variance and $k/\left(n_k+k\right)$ of the break variance to be explained. Because the noise and the break signal are independent, the totally explained variance V(k) can be obtained by a simple addition of Eqs. (5) and (8). Since we consider the difference of two time series the climate signal is assumed to be cancelled out and the total variance is assumed to consist only of these two components, the break and the noise variance ${\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}$ and ${\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}$. In the following we normalize the break and noise variances by the total variance:

$$\begin{array}{}\text{(9a)}& {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}}},\text{(9b)}& {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{2}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}}},\end{array}$$

where the normalized variances are denoted by small instead of capital subscripts. Using the above normalization and replacing ${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{2}}$ with $\mathrm{1}-{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$, we obtain the normalized explained variance V(k):

$$\begin{array}{ll}{\displaystyle }V\left(k\right)& {\displaystyle }={\displaystyle \frac{V_{\mathrm{Bave}}\left(k\right)+V_{\mathrm{Nave}}\left(k\right)}{{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}}}\\ \text{(10)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{k}{n_k+k}}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}+{\displaystyle \frac{k}{n-\mathrm{1}}}\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}\right).\end{array}$$

Equation (10) gives the theoretical expectation. The actually performed test of blindly inserted breaks yields a number of empirical values V_emp(k). These are averaged for each number of breaks k and compared to the theoretical values given in Eq. (10). The magnitude of the two unknowns n_k and ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ are determined by minimizing the squared difference between theoretical and empirical variance. Figure 6 shows the result of applying the procedure to the difference time series of the monthly mean temperature for the climate stations Ellwangen and Crailsheim. Crosses denote the empirical values for the external variance V_emp as derived from the data, to which a curve of the form given in Eq. (10) is fitted in order to obtain estimates for n_k and ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$. The lower of the two increasing lines shows the noise fraction, which grows linearly according to the second summand in Eq. (10). For the upper parallel line, ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ is added so that the constant space between both is giving the pure break variance. For the example given in Fig. 6, the calculations yield ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}=\mathrm{0.226}$ and n_k=3. For $k_{max}=\mathrm{30}$ almost the entire break variance is reached plus a known fraction of noise. At k=n_k half of the break variance is reached as it is expected from Eq. (8).

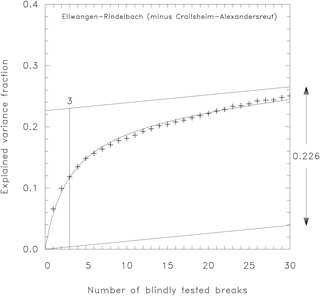
Figure 6 Estimation of break variance (0.226) and number (3) for the station pair Ellwangen-Rindelbach minus Crailsheim-Alexandersreut.

The technical details we used to fit Eq. (10) to the data are the following. We search for the minimum in D, which is defined as the squared difference between the theoretical function given on the right-hand side of Eq. (10) and the empirical data:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }D\left(n_k,{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}\right)=\\ \text{(11)}& {\displaystyle }& {\displaystyle }\sum _{k=\mathrm{1}}^{k_{max}}{\left({\displaystyle \frac{k}{n_k+k}}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}+{\displaystyle \frac{k}{n-\mathrm{1}}}\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}\right)-V_{\mathrm{emp}}\left(k\right)\right)}^{\mathrm{2}}.\end{array}$$

A necessary condition for a minimum in D is that the partial derivation with respect to ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ is zero:

$$\begin{array}{ll}{\displaystyle \frac{\partial D}{\partial {\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}}}& {\displaystyle }=\mathrm{2}\sum _{k=\mathrm{1}}^{k_{max}}\left({\displaystyle \frac{k}{n_k+k}}{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}+{\displaystyle \frac{k}{n-\mathrm{1}}}\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}\right)-V_{\mathrm{emp}}\left(k\right)\right)\\ \text{(12)}& {\displaystyle }& {\displaystyle }\left({\displaystyle \frac{k}{n_k+k}}-{\displaystyle \frac{k}{n-\mathrm{1}}}\right)=\mathrm{0}.\end{array}$$

which can be solved for ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$:

$$\begin{array}{ll}{\displaystyle }{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}& {\displaystyle }={\displaystyle \frac{\sum _{k=\mathrm{1}}^{k_{max}}\left(V_{\mathrm{emp}}\left(k\right)-b\right)\left(a-b\right)}{\sum _{k=\mathrm{1}}^{k_{max}}{\left(a-b\right)}^{\mathrm{2}}}},\text{with}a={\displaystyle \frac{k}{n_k+k}}\\ \text{(13)}& {\displaystyle }& {\displaystyle }\text{and}b={\displaystyle \frac{k}{n-\mathrm{1}}}.\end{array}$$

Equation (13) provides an optimum value for ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ for each potential n_k so that D becomes a function of n_k only. That break number n_k producing a minimum in D is finally chosen as the true (most probable) break number. Since realistic break numbers are equal to a small natural number, only a limited number of tests is necessary.

The above-described procedure, so far shown in Fig. 6 for only one station pair, is now applied to 443 station pairs in Germany (Fig. 7). In some cases the algorithm yields negative values for the normalized break variance. For stations without any inhomogeneity the correct retrieval would be zero break variance. Small random fluctuations of the noise variance can cause a spurious small value for the estimated break variance which may randomly be either positive or negative. Thus, these results are indeed unphysical, but difficult to avoid in statistical approaches with error-affected output. Omitting or setting them simply to zero would bias the result, so that we included them without correction when means over all stations are calculated. On average about six breaks are detected. Please note that we analyzed the difference time series of two stations. Therefore, the double number of breaks arises here. For a single station only about three breaks in 50 years is the correct measure, which is in good agreement with the break frequency (one per 15 to 20 years) found by Menne and Williams (2005). The second target parameter, the break variance fraction, is given on the ordinate of Fig. 7 and is equal to about 0.2 when averaged over all station pairs. Thus, the mean ratio of break and noise variance can be estimated to $\mathrm{0.2}/(\mathrm{1}-\mathrm{0.2})=\mathrm{1}/\mathrm{4}$. Consequently, the signal-to-noise ratio SNR is equal to 1∕2, because it is not defined by the ratios of the variances, but by that of the standard deviations.

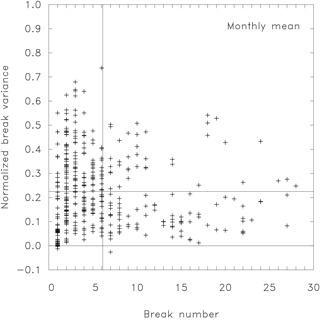
Figure 7 Estimation of the break variance and the number of breaks for monthly mean temperature. The estimation is given for 443 different German station pairs. The vertical line denotes the mean break number (6.1) found for all stations, and the horizontal lines mark zero variance and the average explained normalized variance (0.22), respectively.

In statistical homogenization a range of SNRs will occur. For many climate parameters the SNR can be expected to be even smaller than 1∕2, due to lower spatial correlations, which cause a higher noise level: besides air pressure, the monthly mean temperature is expected to be one of the highest correlated climate parameters. On the other hand, in most of the world and in earlier periods the network density will be lower, which increases the noise and reduces the SNR. Also, indices capturing the statistical distribution (Zhang et al., 2011) could be the target parameter of homogenization, but will generally have lower SNRs. The simplest statistical index is the standard deviation of daily means within the month. If the procedure is applied to this parameter the mean break variance falls below 10 %, which means that the SNR is smaller than 1∕3.

7 What may go wrong in the break detection process?

With Eqs. (5) to (8) we have a tool to retrace the process of break detection in a theoretical manner. Key parameters are the signal-to-noise ratio $\mathrm{SNR}=\sqrt{{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}/\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}\right)}$ and the relative break number $n_k/\left(n-\mathrm{1}\right)$. To illustrate the problem, we chose a low SNR $=\mathrm{1}/\mathrm{3}$ (${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}$ = 0.1) as found for the monthly standard deviation of temperature and n_k=7 breaks within a time series length of n=100 as boundary values. Figure 8a shows the four functions given by Eqs. (5) to (8) for these settings. The external variance for the best break segmentation V_bmax reaches almost the full break variance of ${\mathit{\sigma }}_{\mathrm{b}}^{\mathrm{2}}=\mathrm{0.1}$ well before k reaches n_k, as prescribed by the fourth power function of Eq. (7). The variance for mean break segmentation V_bave reaches half of the break variance at k=n_k (compare Eq. 8). The variance for the best noise segmentation V_nmax is a fifth power function (Eq. 6). However, as n is large compared to k, Eq. (6) can be approximated to $V_{\mathrm{nmax}}=\mathrm{5}k/\left(n-\mathrm{1}\right)$ so that the variance grows approximately linearly with 0.05k. Finally, the variance for an average noise segmentation V_nave is characterized by an exactly linear growth by about 1 % per break (Eq. 5).

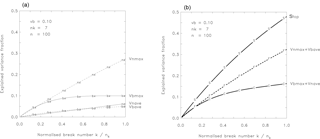
Figure 8 (a) Explained variances as given by Eqs. (5) to (8) for a time series of length 100 containing seven breaks with a SNR of 1∕3. (b) Explained variances as given by Eqs. (5) to (8). As (a), but for the summed up correct ($C=V_{\mathrm{bmax}}+V_{\mathrm{nave}})$ and false ($F=V_{\mathrm{nmax}}+V_{\mathrm{bave}}$) combinations, and the stop criterion (S), which has to be exceeded.

Applying a reasonable break search algorithm for an increasing number of k, the explained variance is expected to follow largely V_bmax. However, it is unavoidable that at the same time also a small part of the noise is explained just by chance. This additional contribution is given by the variance for mean noise V_nave. Thus, a correct segmentation will combine V_bmax (Eq. 7) and V_nave (Eq. 5), given by the two solid lines in Fig. 8a. But there is also the reverse alternative. This is the (false) combination of the best noise variance V_nmax (Eq. 6) and the mean break variance V_bave (Eq. 8), depicted as dashed lines in Fig. 8a. In this case, only the noise is optimally segmented; however, a considerable part of the breaks is just accidentally explained by V_bave. Figure 8a shows that the best noise variance V_nmax is generally larger than the best break variance V_bmax, while the two mean contributions V_bave and V_nave are of a comparable and small size. Consequently, it is clear that, with the chosen features, the false combination explains for every break number more variance than the correct one.

However, break search algorithms always contain a stop criterion, which may in this case reject any segmentation at all, in this way preventing these wrong solutions. The argument of the Caussinus–Lyazrhi stop criterion given in Eq. (4) becomes zero for k=0 (as the explained variance V(k) is then trivially also zero). Obviously, this zero solution is identical to the required minimum, if the expression becomes positive for all remaining (positive) k. In this case the search is stopped at k=0 and the algorithm output will be that there is no break in the time series. So, in turn, a necessary condition for an actually existing break is that the argument is somewhere negative:

$$\begin{array}{}\text{(14)}& {\displaystyle }\ln \left(\mathrm{1}-V_{max}\left(k\right)\right)+{\displaystyle \frac{\mathrm{2}\ln \left(n\right)k}{n-\mathrm{1}}}<\mathrm{0},\end{array}$$

which can be solved for V_max,

$$\begin{array}{}\text{(15)}& {\displaystyle }{V}_{max}\left(k\right)>\mathrm{1}-\exp \left(-{\displaystyle \frac{\mathrm{2}\ln \left(n\right)k}{n-\mathrm{1}}}\right),\end{array}$$

and transformed to

$$\begin{array}{}\text{(16)}& {\displaystyle }{V}_{max}\left(k\right)>\mathrm{1}-n^{-\frac{\mathrm{2}k}{n-\mathrm{1}}}.\end{array}$$

The right-hand side expression of inequality Eq. (16) is added in Fig. 8b as a stop criterion. Only solutions exceeding this stop criterion will be accepted. A further modification in Fig. 8b (compared to Fig. 8a) is that both dashed and solid line pairs are summed up to only one function, respectively, i.e., the correct ($C=V_{\mathrm{bmax}}+V_{\mathrm{nave}}$) and the false ($F=V_{\mathrm{nmax}}+V_{\mathrm{bave}}$) solutions. The false solution explains indeed more variance than the correct one, but it seems that the stop criterion is actually preventing (on average) both the false and the correct solutions, because the false solution also does not exceed the stop criterion. However, we will see in the following that this is not always the case.

So far, we considered only the two extreme cases. On the one hand the completely wrong solution, which decomposes the noise optimally and gains some extra break variance just by chance; and on the other hand the completely correct solution, where it is vice versa. We showed that the false combination explains on average more variance and is therefore preferred in the discussed case where the SNR is as small as 1∕3. However, search algorithms select the best segmentation explaining the most variance. This solution may lie between the two extremes. We will study next whether this actually chosen solution primarily explains the breaks or the noise.

For this purpose, we created an ensemble with 1000 simulated time series of length 100 with seven breaks at random positions. Both noise and break variance are Gaussian, with a magnitude of unity for the breaks and 9 times larger for the noise, so that the signal-to-noise ratio is 1∕3. For each individual time series the optimal solutions for the number of breaks from one to seven are determined by optimal partitioning. Then we computed the explained variance for the entire time series and additionally the explained noise and break parts separately. Finally we averaged over the ensemble for each break number class. Figure 9a shows the resulting graphs. The first, marked by (1), shows the explained break variance, (2) the explained noise part, and (3) the sum of the two. The fourth of the thick curves gives the total explained variance. Additionally, three thin auxiliary lines are drawn. The first two show the theoretical results for random breaks (V_Bave) and best noise (V_Nmax) as given by Eqs. (8) and (5), respectively. The third curve gives the stop criterion (Eq. 16). It is striking that the found break variance (1) is hardly larger than the theory for random breaks predicts (V_Bave), and the noise variance (2) nearly attains the theoretical value for optimal noise decompositions V_Nmax. Thus, the segmentations explaining most variance, which are actually selected by the break search algorithms, are very similar to the false combination.

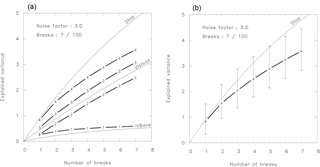
Figure 9 (a) Explained variances of breaks and noise, and the total explained variance, calculated from 1000 realizations. The explained variance for the breaks only is denoted by 1, the noise only by 2, the sum of these two terms by 3, and the total explained variance by 4. Equations (6), (8), and (16) are given as thin lines for orientation showing V_Nmax, V_Bave, and the stop criterion, respectively. (b) As (a), but including also the variability of curve 4 and omitting the other curves. The whiskers denote the 1st and 9th deciles, respectively.

A second feature in Fig. 9a needs to be discussed. The total explained variance (4) is larger than the sum of explained break and noise variance (3). As the best segmentation (in terms of explaining the total variance) is always chosen, solutions dominate, where (the external) break and noise variances are slightly correlated. In order to explain a maximum of variance it is advantageous to cut the time series in such a way that both break and noise variance are high. In this way correlated segments are preferred. These correlations enhance the average total explained variance further. It is, however, apparently not strong enough to exceed the stop criterion, given by the upper thin line in Fig. 9a.

However, so far we have considered only the means over 1000 realizations. But these solutions are varying, so that the threshold is often exceeded, at least for low break numbers. In Fig. 9b we show only curve (4), the total explained variance, but added as whiskers the 1st and 9th deciles to give an impression of the variability of the solutions.

In Sect. 6 we found that the SNR is less than 1∕3 for the standard deviation of the daily temperature within the months. For this SNR we showed in this section that the correct break combination explains less variance than the completely false one, which is defined by decomposing only the noise optimally. Break search algorithms always select the decomposition that explains most of the variance. These solutions are shown to be rather similar to the noise optimizing decomposition. In this light it may be doubted whether break detection is feasible at all for these (realistic) SNRs far below 1 for low n (e.g., n=100). In the following section we will thus investigate how useful the maximum external variance is as a break criterion.

8 Skill of the search method

In multiple breakpoint methods the maximum explained variance determines the position of the breaks. In this section we want to make the case that this variance may not be a good measure at low SNRs, while it works well for large SNRs.

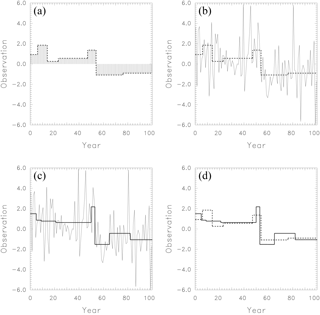
Figure 10 Illustration of the skill measure M2, the mean squared deviation between estimated and true break signals. (a) The time series of inhomogeneities is interpreted as a signal to be detected (dashed step function). (b) The detection of the signal (dashed step function) is hampered by superimposed scatter. (c) Homogenization algorithms search for the maximum external variance of the noisy data. The corresponding estimated signal (step function) is given by the thick line. (d) The mean squared difference between true (dashed) and estimated (solid) signals is an appropriate skill measure.

Consider the difference time series of two neighboring stations. One part consists of the inhomogeneities that we want to detect. This time series component is the signal. Figure 10a shows a simulated example of such a time series. We inserted seven breaks with a standard normal distribution at random positions. In reality, the detection of the breaks is hampered by superimposed noise, which is caused by observation errors and different weather at the two stations. To simulate this, we added random noise (Fig. 10b) with a standard deviation of 2, which corresponds to a SNR of 1∕2. Homogenization algorithms search for the maximum external variance of the entire noisy data consisting of both breaks and noise. The obtained result is then the estimated signal. For illustration we show the optimum solution for the arbitrarily chosen seven breaks given in Fig. 10c by the solid step function. In Fig. 10d we compare the true and the estimated signal. Their mean squared difference is an appropriate skill measure of the applied break search. So we have two measures:

•  

  M1: the total variance explained by test breaks in the noisy data;

•  

  M2: the mean squared deviation between the estimated and true signals.

Maximum M1 is used in the homogenization method to define the optimum segmentation and in this way the position of the breaks. M2 is equal to the residual error, so that its minimum is a good indicator for the true skill of the method. For real cases, M1 is the only available measure, because the true signal is not known. Only with simulated data we are able to compare M1 and M2. Hereby, we are able to assess the segmentation usually selected, by the appropriate, but usually unknown skill measure M2. We proceed from very simple search settings to the most sophisticated one, which is described in Sect. 4 as the break search method.

As a first approach, we take one simulated time series (length 100 including seven true breaks at random positions with SNR $=\mathrm{1}/\mathrm{2}$) and calculate the explained variance also for seven random test break positions. The procedure of randomly chosen test break positions is repeated 100 times so that 100 pairs of M1 and M2 are available (Fig. 11a). This is indeed a simplistic search, but hereby we are able to consider the whole variety of solutions, whereas in the actually applied search (using optimal partitioning) only the resulting optimum is available. In Fig. 11a we marked the best solution in terms of M1 (i.e., a lower estimate for the result of a breakpoint detection method) with a circle and that in terms of M2 (the actual best one) with a cross. The two points are widely separated, showing that a very simple search approach (best of 100 random trials) would theoretically be able to provide rather good solutions (M2 = 0.15). However, the correlation with M1 is low, so that a decision made by M1 (circle) leads to rather unskilled solutions (M2 = 0.60).

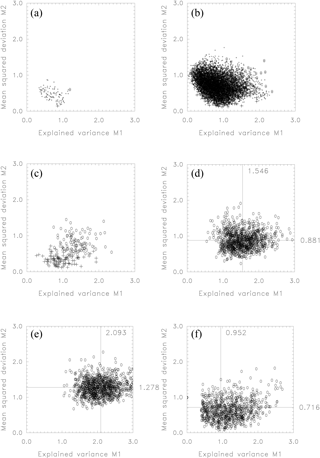
Figure 11 Mean squared signal deviation (M2) against explained variance of the noisy data (M1). These two measures are given for random segmentations of simulated time series of length 100 with SNR $=\mathrm{1}/\mathrm{2}$, with seven true and seven tested breaks. (a) 100 random segmentations of a single time series. (b) As panel (a), but for 100 segmentations of 100 time series. (c) As panel (b), but only for the maxima with respect to the explained variance (0) and with respect to the true skill (+). (d) As panel (c), but the number is increased from 100 by 100 to 1000 by 1000 and only the maxima with respect to the explained variance (0) are drawn. The horizontal and vertical lines give the means for the two axes. (e) As panel (d), but here the maximum explained variance is searched by optimal partitioning (without a stop criterion) instead of just choosing the best of 1000. (f) As panel (e), but for the full search method (optimal partitioning plus a stop criterion). The estimated break number is no longer fixed to be seven, but is defined by the stop criterion given in Eq. (4).

In Fig. 11b we repeat the exercise for 100 instead of only 1 time series to not be dependent on just one single time series with possibly extraordinary features. The solution cloud shows again that the correlation between M1 and M2 is low. Now we have 100 circles and 100 crosses for the maximum explained variance and the really best solutions, respectively. For a better visibility the rest of the cloud is omitted in Fig. 11c. It shows that circles are generally located higher than crosses, indicating their lower skill.

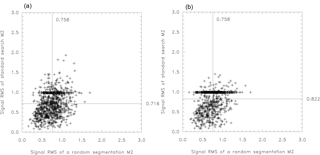
Figure 12 (a) Skill of the search method versus an arbitrary segmentation for seven breaks within 100 time steps and SNR $=\mathrm{1}/\mathrm{2}$. As (a) but with stop criterion increased by a factor of 1.5.

In the next step, we increase the number from 100 to 1000 series. Thus, now we create 1000 time series and test each of them with 1000 random break combinations consisting always of seven breaks (Fig. 11d). Here, only the circles are shown, the normally proposed solutions, determined by the maximum explained variance. The mean of the explained variance over all 1000 of these maxima is 1.546. The corresponding true skill is defined by the position on the ordinate, which is on average 0.881. We can conclude that for a simplistic search (best of 1000 random trials) the explained variance is higher than the originally inserted one (1.546 vs. 1.0), and that the error index (0.881) does not differ substantially from the one actually included in the series (1.0), standing for no skill at all.

In the next step we use optimal partitioning (for now without any stop criterion) to find the maximum explained variance (Fig. 11e), instead of choosing the highest of 1000 random trials. The explained variance increases as the used method is of course more powerful. Now, the explained variance is as high as 2.093. However, also the mean signal deviation increases from 0.881 (Fig. 11d) to 1.278. Such a value, larger than 1, indicates that this is worse than doing nothing. In some sense, we may conclude that the simplistic search (best of 1000) has a better performance than the sophisticated technique of optimal partitioning. This result can be explained as follows. Optimal partitioning indeed provides the optimum result for the maximum variance. But this parameter is only loosely coupled to the true skill. Due to the presence of noise, the estimated signal has a much too large variance and is at the same time only weakly correlated with the true signal, so that also the deviation of the two signals M2 is further increased. The underlying reason for this worsening is that, up to now, we did not include the normally used stop criterion. Instead we searched for the best solution for seven breaks, corresponding to the true number hidden in the time series.

Consequently, we finally added the stop criterion given in Eq. (4). Thus, we finally applied the full search method described in Sect. 4, which consists of two steps: first, the maximum external variance is determined by optimal partitioning for all possible break numbers; then a stop criterion is used to determine the correct break number (Fig. 11f). Thanks to the stop criterion, only in 9.8 % of the cases is the final error higher than the original one (M2 >1), while, using the former implementation without a stop criterion (Fig. 11e), this percentage was as high as 88 %. Thus, we can further conclude from Fig. 11e that searching until the true number of breaks is reached will produce very poor results. So, even if the true number of breaks is known in advance, trying to detect all breaks is not the right approach.

In Fig. 11f the mean signal deviation attains at 0.716 again a value below the no-performance threshold of 1. Also, the mean explained variance is decreased to 0.952. This is due to the introduced stop criterion, which enables the algorithm to produce solutions with fewer breaks. The zero solutions without breaks are concentrated at the point (0.0; 1.0), because no variance is explained and the signal deviation is as large as the signal variance itself. However, at 0.716 the mean skill is still poor.

8.1 Comparison of the applied search method with random segmentations

To decide whether this skill is better than random, we use again the simulated data discussed above. As in Fig. 11f, we calculate for each of the 1000 random time series the mean squared deviation between the true and estimated signals for the search method. But now this search skill is compared to the same measure obtained for a random decomposition (of the same time series) by seven breaks. The resulting 1000 data pairs of search skill with its counterpart from a random decomposition are given in Fig. 12a. Zero break solutions (only produced by the actual search method) can be identified as a marked horizontal line at y=1. The principal conclusion is that the skills of the search method (0.716) and an arbitrary segmentation (0.758) are quite comparable. This suggests that the search method mainly optimizes the noise explanation, producing in this way random results.

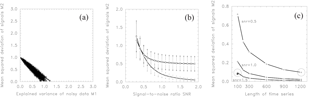
Figure 13 (a) Mean squared signal deviation (M2) against explained variance of the noisy data (M1) for 100 random segmentations of 100 simulated time series with length 100, including seven true breaks and tested by the same number of breaks. As Fig. 11b, but for SNR =2. (b) Mean squared deviation between true and estimated break signal M2 for simulated time series of length 100, including seven breaks averaged over 1000 repetitions. Skill M2 is given as a function of the signal-to-noise ratio for two cases: search method (crosses) and random segmentation (circles). The standard deviations for both cases are given as whiskers. (c) Mean squared deviation of signals M2 as a function of series length for three different SNRs (0.5, 1.0, and 1.5). The mean deviation M2 of each length class and SNR is obtained by 1000 repetitions. Two specific values (SNR =1.5, n=100) and (SNR =0.5, n=1200) are marked by circles and discussed in the text, as well as the filled square denoting data which are directly averaged from n=1200 to n=100 for SNR =0.5.

We thus showed that a signal-to-noise ratio of 1∕2 is too low for a reasonable break search by a multiple breakpoint homogenization algorithm. Several significant breaks are reported, although their positions cannot be distinguished from random ones. In this situation it is clear that the number of reported breaks has to be reduced. Consequently, we increased the stop criterion by a factor of 1.5 by changing the original constant in Eq. (4) from 2 ln(n) to  3 ln(n). As a result the average signal deviation increases from 0.716 to 0.822 (compare Fig. 12a and b). The reason is that more zero break solutions are produced (with a root mean square error of 1), which are not compensated for by more accurate non-zero solutions, so that an overall worse skill results.

Thus, for SNR =0.5 and series lengths of n=100, the two measures M1, which is the parameter maximized in break search methods and M2, representing the true error variance, are only weakly correlated. Consequently, the residual error of segmentations obtained by the homogenization method is essentially similar to that of the random segmentations. Increasing the strength of the stop criterion does not produce a better detection skill on average, but it reduces the fraction of cases where the residual error is larger than the original.

8.2 Higher SNRs

So far we have considered SNRs of 1∕2. In the following, we increase the SNR to 2, having now the opposite relation: the noise is half of the amount of the breaks. In this case, the (negative) correlation between M1 and M2 is strongly increased (Fig. 13a). If no variance is explained the mean square deviation from the signal is 1, and vice versa: explained variances around 1 have generally a deviation near 0. Thus, in this case the inherent assumption of high (negative) correlation between the two measures M1 and M2 holds true. Consequently, the used search method provides good results. For this SNR of 2 the mean deviation from signal decreased to 0.049 (not shown) compared to 0.716 for SNR $=\mathrm{1}/\mathrm{2}$ (Fig. 12a).

To study the relationship between SNR and break detection skill, we repeated the calculations for different SNRs between 0.3 and 1.9. The residual errors M2 for both random segmentation (circles) and search method (crosses) are given in Fig. 13b. As a guide for the eye, two thick connecting lines are drawn. The standard deviations of the two skills resulting from 1000 repetitions are given by vertical whiskers. At SNR =0.5 the two mean skills are almost equal, at 0.713 and 0.756 (these values are identical to those shown in Fig. 12a). For higher SNRs the two curves diverge. The random segmentation curve approaches a constant value near 0.5, whereas the mean squared deviation for the search method decreases asymptotically to zero. The fast transition from reasonable to nearly useless makes an a priori assessment of the SNR, as it is presented in Sect. 6, advisable.

8.3 Yearly and monthly resolution

However, the SNR is not a fixed characteristic for a given dataset. It depends on the temporal resolution in which the data are used. Aggregating monthly data to yearly resolution, e.g., will increase the SNR but decrease the sample size. Both SNR and sample size affect the detection power (see the next paragraph for the latter effect). The reason is that the effect on the break variance part remains small, whereas the noise part decreases rapidly by averaging over 12 months: under the (reasonable) assumption that the noise part of the difference time series is weakly correlated, the variance is reduced by a factor of 12. To estimate the reduction of break variance, we can use Eq. (8), setting k to the number of years the time series comprises. For n_k=5 breaks within 100 years, we obtain a remaining variance fraction of 100∕105; thus, only about 5 % of the break variance is lost by the averaging process. The relation between the signal-to-noise ratio on a yearly basis SNR_y and its monthly counterpart SNR_m can be estimated to

$$\begin{array}{}\text{(17)}& {\displaystyle }{\mathrm{SNR}}_{\mathrm{y}}\approx \sqrt{{\displaystyle \frac{\mathrm{0.95}{\mathit{\sigma }}_{\mathrm{B}}^{\mathrm{2}}}{\frac{{\mathit{\sigma }}_{\mathrm{N}}^{\mathrm{2}}}{\mathrm{12}}}}}=\mathrm{3.4}{\mathrm{SNR}}_{\mathrm{m}}.\end{array}$$

Thus, we can expect that the SNR of yearly data will be increased by a factor of 3 to 4 compared to monthly resolution. Conversely, the SNR of daily data will be much lower.

These considerations suggest that SNR and series length are mutually dependent. Averaging monthly data to yearly resolution reduces the length formally by a factor of 12, while increasing vice versa the SNR by a factor of about $\sqrt{\mathrm{12}}$. If we assume that purely averaging from monthly to yearly resolution does not change the general skill of the detection method, these two effects must compensate each other.

To study this conjecture we investigate the influence of series length on the detection skill by repeating the calculations for varying lengths from 100 to 1200, while holding the SNR constant. Figure 13c shows the result for SNR =0.5 (upper curve). The mean squared deviation of signals M2 decreases with growing length from 0.716 (for 100 data points) to 0.097 (for 1200 data points). For SNR =1.0 (middle curve) the deviation M2 is generally reduced by a factor of about 4. For 100 data points we found M2 =0.212 decreasing to M2 =0.022 for 1200 data points. The lower curve shows the results for SNR =1.5. The deviation M2 is further reduced to 0.093 (for 100 points) and 0.009 (for 1200 points). The comparison of two particular values (marked by circles in Fig. 13c) is of specific interest: the deviation for 100 points and SNR =1.5 with that of 1200 points and SNR =0.5. With 0.097 and 0.093, respectively, they are rather similar in size. This confirms our estimation made in Eq. (17) that 3-fold SNR has a comparable impact as a 12 times longer time series, as is the case for monthly data. There is a third particular data point, marked by a filled square in Fig. 13c. Here monthly time series of length 1200 with SNR =0.5 are directly averaged to yearly resolution (with length 100). The resulting skill remains fairly similar. This implies that it does not matter much at which resolution a given time series is homogenized: the opposite effects of reduced length and increased SNR are largely cancelled out.

For a given SNR there is a minimum series length for reliable analysis. Redoing periodically the changepoint analysis can improve the results as the series lengths usually increase yearly.

9 Conclusions

Multiple breakpoint homogenization algorithms identify breaks by searching for the optimum segmentation, explaining the maximum of variance. In order to assess the performance of this procedure, we decomposed the total variance of a difference time series into two parts: the break and the noise variance. Additionally, we distinguished between the optimal and arbitrary segmentations. In Eqs. (5) to (8) we give formulae for all four cases, describing how the explained variance grows when more and more breaks are assumed.

With this concept it is possible to determine the SNR of a time series in advance without having to apply a statistical homogenization algorithm. For the monthly mean temperature of German climate stations, which are characterized by a high station density, we found a mean SNR of 0.5, which corresponds to a SNR on annual scale of about 1.5. Even for such small inhomogeneities, the inhomogeneity-induced spurious trend differences between neighboring stations are strong and homogenization important. The signal-to-noise ratio in earlier periods and non-industrialized countries will often be lower due to sparser networks. Also, other statistical properties than the mean (Zhang et al., 2011) will in general have lower correlations and more noise. For the monthly standard deviation of temperature, we found a SNR of 1∕3.

For SNRs below 1, the multiple breakpoint search algorithm fails under typical conditions assuming seven breaks within a time series of length 100. The reason is that random segmentations are able to explain a considerable fraction of the break variance (Eq. 8). If the tested number of breaks is comparable to the true one, they explain about one-half. Consequently, the estimated breaks are not set according to the true breaks, but to positions where a maximum of noise is explained. Hereby, the explained noise part is increased by a factor of 5. Thus, if the noise is large, systematic noise explanation is unfortunately the best variance maximizing strategy. At the same time the signal part is small and its explained variance decreases in return only by a factor of 2, i.e., from 1 for the optimum to 1∕2, which is attainable just randomly.

Considering the time series of inhomogeneities as a signal that shall be detected, we define the mean squared difference between the true and estimated signals as a skill measure. In the case of simulated data, this measure can be compared to the explained variance, which is used normally to select the best segmentation. While for high SNR the two measures are well correlated, their correlation is weak for a SNR of 1∕2. Consequently, large detection errors occur. Even a random segmentation attains almost the same skill as the applied search method. The reason is the following: the variance explained by an optimal segmentation of the noise alone is not sufficient to exceed the significance threshold. However, the same segmentation explains large parts of the break variance even if the tested break positions are far away from the true ones. The combination of both optimized noise and random break variance is unfortunately large enough to exceed the significance threshold in many cases. The wrong solution is accepted and there is no indication that the method is failing.

A stronger stop criterion to purely suppress the majority of the wrong solutions is shown to be not helpful. The presented new method to estimate the break variance and number of breaks might be useful for a future better stop criterion.

If the SNR becomes larger than 0.5, the situation improves rapidly and above a SNR of 1 break detection performs reasonably. The SNR of the HOME benchmark dataset was on average 1.18 for monthly data (corresponding to about 3.5 for annual data), but the break sizes were found to be too high in the validation of the benchmark (Venema et al., 2012). Our study confirms that a good performance of the tested homogenization method can be expected under such circumstances. For lower SNRs, as we found them in German climate stations on monthly resolution, the results may differ.

In future, the joint influence of break and noise variance on other break detection methods should be studied. One would expect that also other methods would need to take the SNR into account. However, the validation study of several objective homogenization methods by Domonkos (2013) shows that while the multiple breakpoint detection method of PRODIGE is best for high SNR, for low SNR many single breakpoint detection methods are obviously more robust and perform better.

Furthermore, the influence of the signal-to-noise ratio on full homogenization methods, including also the data correction, should be tested. The benchmarking study of HOME has shown that there is no strong relationship between detection scores and climatologically important validation measures, such as trend error or root mean square error. For example, PRODIGE was here among the best methods, but performed only averagely with respect to the detection scores. Thus, the consequences for climatologically important error measures are not trivially obvious.

This study finds that SNR and series length are connected. For sample sizes of 100, it is important to achieve a SNR above one. It would thus be worthwhile to develop methods that reduce the noise level of the difference time series. And of course, in case of low SNRs the use of metadata on the station history will be particularly valuable.

Finally, this study shows that future validation studies should use a (realistic) range of SNRs. The International Surface Temperature Initiative aims at computing the uncertainties remaining in homogenized data and will perform a benchmarking mimicking the global observational network, which therefore includes a realistic range of SNRs (Willett et al., 2014; Thorne et al., 2011).