the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Identifying time patterns of highland and lowland air temperature trends in Italy and the UK across monthly and annual scales
Chalachew Muluken Liyew
Elvira Di Nardo
Rosa Meo
Stefano Ferraris
This paper presents a statistical analysis of air temperature data from 32 stations in Italy and the UK up to 2000 m above sea level from 2002 to 2021. The data came from both highland and lowland areas in order to evaluate the differences due to both location and elevation. The analysis focused on detecting trends at annual and monthly timescales, employing ordinary least-squares (OLS), robust S-estimator regression, and Mann–Kendall (MK) and Sen's slope methods. Hierarchical clustering (HCA) using dynamic time warping (DTW) was then applied to the monthly data to analyze the intra-annual pattern similarity of trends within and across the groups.
Two different regions of Europe were chosen because of the different climate and temperature trends – namely, the northern UK (smaller trends) and the northwest Italian Alps (larger trends). The main novelty of the work is to show that stations with similar locations and altitudes have similar monthly slopes by quantifying them using DTW and clustering. These results reveal the nonrandomness of different trends throughout the year and between different parts of Europe, with a modest influence of altitude in wintertime. The findings revealed that group average trends were close to the National Oceanic and Atmospheric Administration (NOAA) values for the areas in Italy and the UK, confirming the validity of analyzing a small number of stations. More interestingly, intra-annual patterns were detected commonly at the stations of each of the groups and are clearly different between them. Confirming the different climates, most highland and lowland stations in Italy exhibit statistically significant positive trends, while in the UK, both highland and lowland stations show statistically nonsignificant negative trends. Hierarchical clustering in combination with DTW showed consistent similarity between monthly patterns of means and trends within the group of stations and inconsistent similarity between patterns across groups. The use of the 12 distance correlation matrices (dcor) (one for each month) also contributes to what is the main result of the paper, which is to clearly show the different temporal patterns in relation to location and (in some months) altitude. The anomalous behaviors detected at 3 of the 32 stations, namely Valpelline, Fossano, and Aonoch Mòr, can be attributed, respectively, to the facts that Valpelline is the lowest-elevation station in its group; Fossano is the southernmost of the Italian stations, with some sublittoral influence; and Aonoch Mòr has a large number of missing values.
In conclusion, these results improve our understanding of temperature spatio-temporal dynamics in two very different regions of Europe and emphasize the importance of consistent analysis of data to assess the ongoing effects of climate change. The intra-annual time patterns of temperature trends could also be compared with climate model results.
- Article
(3584 KB) - Full-text XML
- BibTeX
- EndNote
The study of climate variability and its impact on our environment has garnered increasing attention in recent years driven by growing concerns over the consequences of global climate change. The study of air temperature is a crucial aspect of climatology that is widely examined worldwide, with the Intergovernmental Panel on Climate Change (IPCC) stating that warming is not observed or expected to be spatially or seasonally uniform (Collins et al., 2013). In fact, global warming is modulated by external forcing (“signals”) and internal variability (“noise”) (Li et al., 2022). There are many goals of comprehending its ever-changing nature in various regions over different time frames, with many examples (Farooq et al., 2021; Khavse et al., 2015). Globally, there is a consistent upward trend in air temperatures (Simmons et al., 2021). This phenomenon is not limited to global observations alone; it is also evident at regional levels as seen, e.g., throughout Europe, where air temperatures have displayed a continuous linear increase since 1985 (Twardosz et al., 2021), and in the central Asian region (Farooq et al., 2021). A time trend that appears to be mainly positive and reveals a significant rise in temperature was detected by Gil-Alaña et al. (2022) when aggregated monthly temperature data were analyzed from 48 contiguous US states. Furthermore, when disaggregated data on temperature anomalies were considered at the state level, a large number of states showed a significantly positive temporal trend coefficient. Remarkably, this trend turned out to include seven exceptions, all of which occurred in the southeast. Also, 309 stations in Canada and the US were examined in Isaac and Van Wijngaarden (2012), revealing significant warming trends, particularly in the midwestern US, Canadian prairies, and western Arctic, primarily in winter and, to a lesser degree, in spring. A dataset from 19 stations ranging from 1920 to 2006 was analyzed in El Kenawy et al. (2012), and the result was a significantly increased trend in maximum, minimum, and average temperatures, especially since 1960. The annual trend was explored in Di Bernardino et al. (2022) using data obtained from three stations in Rome (Italy) in the period from 2000–2020 and identified a statistically positive trend of annual mean temperatures.
However, a warming hiatus occurred in the period from 2004–2018 in the Northern Hemisphere, especially in autumn and in more northern areas (Tang et al., 2022; Shen et al., 2018). Before those years of hiatus, a study conducted in the US did an interesting combined analysis of the pattern of temperature trends during the months and during the days (Vinnikov et al., 2002). The analyses of that paper were not repeated in other papers, and, in our opinion, they deserve to be repeated with more recent data in order to see if less noisy patterns can emerge. Instead, many papers addressed the topic of the trends in the diurnal temperature range (DTR; for example, Shen et al., 2014). Annual and seasonal averages of DTR and maximum and minimum temperatures were considered by Sayemuzzaman et al. (2015) using 249 stations (1950–2010) in North Carolina, and the result showed a negative annual trend in the diurnal temperature range and a positive trend for maximum and minimum temperatures, which were statistically significant. The maximum temperature showed a negative trend during summer and spring and a positive trend during the autumn season, the minimum temperature showed an increasing trend in all seasons, and the diurnal temperature range showed a decreasing trend in all seasons. Notably, temperature extremes have become more frequent and intense throughout Europe in recent decades (Patterson, 2023). According to Patterson (2023), based on ERA5 reanalysis data from 1960 to 2021, the hottest summer days in northwestern Europe are warming up at about twice the rate of average summer days. Additionally, the pattern is relatively unique when compared to the Northern Hemisphere. Another extensively addressed topic is altitude-dependent warming. It occurs throughout the world's highland regions, with the Alps proving to be a notable hotspot for global warming (MRI, 2015). A study looking at the French Alps and adjacent areas in neighboring Italy and Switzerland found a clear overall trend indicating an increase of about 1 °C in annual air temperature over 44 years, with large variations in this trend for different altitudes, seasons, and regions. The trends are most pronounced between 1500 and 2000 m above sea level (a.s.l.) (Durand et al., 2009). A recent paper describes in depth the physical mechanisms driving elevation-dependent warming (EDW) in the tropics and subtropics, highlighting some drivers and, interestingly for our study, monthly variations (Byrne et al., 2024). Available observations suggest that Mediterranean mountains are experiencing seasonal warming rates that are largely greater than the global land average. The identification and attribution of human versus natural effects is beyond the scope of this paper. For example, a human fingerprint (Blackport et al., 2021) in the decreasing subseasonal near-surface air temperature variability has recently emerged from a reanalysis of the Northern Hemisphere extratropics. It features decreased near-surface air temperature variability over land in the high northern latitudes in autumn, further extending into mid-latitudes in winter. Therefore, using large ensembles of single-forcing model experiments, they attributed the pattern of reduced temperature variability primarily to increased anthropogenic greenhouse gas concentrations, with anthropogenic aerosols playing a secondary role.
In the literature, trends of time variables can be detected, estimated, and predicted using both parametric and nonparametric methods. Parametric methods, such as linear regression, robust regression, moving averages, or multiple regression, require validation of assumptions about the underlying distribution. For example, parametric methods were applied in Vinnikov et al. (2002) to study the diurnal and seasonal cycles of trends in surface air temperature as well as in El Kenawy et al. (2012) to quantify the seasonal and annual trends. Nonparametric methods, on the other hand, do not require assumptions about the underlying distribution but ensure the robustness of the final conclusions. Among nonparametric methods, the most widely used are the Mann–Kendall (MK) test and Sen's slope estimator (Di Bernardino et al., 2022; Mohsin and Gough, 2010; Sayemuzzaman et al., 2015) since these methods are particularly suited for non-normally distributed data even in the presence of missing values. Specifically, the MK test is used to detect the presence of trends in the investigated variables, and Sen's slope estimator estimates the magnitude of these trends. These methods have been widely used in numerous studies aimed at identifying and estimating trends in annual, seasonal, and monthly temperatures in various countries and regions. All these results show that the trends of increasing monthly, annual, and seasonal temperatures are not homogeneous: in some regions, the increase was statistically significant, while in other regions, statistical significance was not reached. Cluster analysis was performed by Rebetez and Reinhard (2008) in Switzerland, showing a difference between low- and high-elevation stations.
In this work, we considered a limited number of stations (32) for the sake of clarity of the proposed method of analysis. Regarding the limited number of years (20), we wanted to limit inhomogeneities in instrumentation, land use, and nonlinearity of trends. The nonlinear behavior of the last few decades is also confirmed by the fact that Brunetti et al. (2006) have shown different Italian historical station trend results, only adding 8 more recent years in the series in comparison with their previous analysis. In order to compare different areas and different altitudes, the attention is focused on six groups of stations over the period from 2002–2021: 11 Italian highland stations (IH), 12 Italian stations at low altitudes (IL), five UK highland stations (UKH), and four low-altitude ones in the UK (UKL). Italian stations (both lowlands and highlands) were further stratified by distinguishing between those in the Valle d'Aosta and those in Piemonte for a total of six different regions. The highland stations are between 1029 and 2017 m a.s.l. in Italy and between 773 and 1237 m a.s.l. in the UK. The lowland stations are between 232 and 577 m a.s.l. in Italy and between 140 and 249 m a.s.l. in the UK. Temperature trends are analyzed at annual and monthly timescales.
The objective of this study is preliminarily to assess trends in six Italian and UK groups of stations, examining the differences between parametric and nonparametric methods in quantifying air temperature trends and exploring the implications of these different methods. For this purpose, Shapiro's test is applied to test the hypothesis of the normal distribution when necessary, as suggested by Royston (1982). After that, the main objective is to analyze the intra-annual pattern similarity of trends within and across these groups of stations in order to assess the role of elevation and geographical location at small and large distances. Regarding elevation, three of them are in the highland region and three are in the lowland region. Regarding the geographical location, two are from the UK, a region with low time variation in temperature, and four are in the Alps, a hotspot of global warming. Also, two different subregions in the Alps are considered in order to see the effect of small geographical distance with respect to the long distance between the UK and Italy. Finally, hierarchical clustering (HCA) and distance correlation are used to identify pattern similarity.
The paper is organized as follows: the dataset is presented in Sect. 2 along with a brief summary of the methods employed for the analysis. Results and discussion are reported in Sect. 3. Some concluding remarks are given in the final section.
2.1 Study area and dataset
This study uses air temperature data obtained from 32 stations located in different geographical areas. The dataset includes observations from highland and lowland stations in the UK and Italy. Specifically, five UK highland stations, four UK lowland stations, 11 Italian highland stations, and 12 Italian lowland stations were chosen to examine and analyze monthly and intra-annual patterns of air temperature trends. The geographical area locations of the study are shown in Fig. 1.
Figure 1The geographical distribution of all stations of (a) Italian highland and lowland and (b) UK highland and lowland considered in this study.
These observations cover the time frame from 2002 to 2021. Annual and monthly trends are calculated only over 20-year periods because of accelerated warming in the Alpine region (Mudelsee, 2019), especially where trends are larger. Also, in the 1990s, measurements shifted from mechanical instruments in shelters to small electronic sensors. At all of these stations, temperature records were collected at half-hourly intervals, totaling 350 640 records for the Italian lowlands, and at 1-hourly intervals, totaling 175 320 records for the highland stations in Italy and the UK as well as all lowland stations in the UK. The location and altitudes of each station in the dataset are given in Table 1.
There are instances of missing values in the dataset, and their proportions in relation to each station can be found in the final column of Table 1. The occurrence of missing values at Italian stations is minimal, while highland stations in the UK have a relatively higher percentage of missing values. Despite these variations, the total number of air temperature observations is sufficiently large, and the limited presence of missing values and their random occurrence in the dataset ensures that their influence on the analysis remains marginal. Given the small number of missing values, the classic seasonally segmented missing-value imputation technique1 was employed. When used as a pre-processing step, this method involves segmenting the time series into seasonal blocks after which imputation is performed individually for each block using interpolation algorithms. After incorporation of the imputed values, the dataset was further processed into monthly and annual time series as presented in the following section.
2.2 Methods
2.2.1 Parametric and nonparametric methods for temperature trends
In this section, we briefly recall the parametric and nonparametric methods used to detect and quantify monthly or annual mean temperature trends as set out in the second part.
For linear regression2, the monthly and annual mean temperature yt (in degrees Celsius) is regressed on the explanatory variable t (month or year, respectively). That is, ; see, for example, Hyndman and Athanasopoulos (2018). Positive values of slope β show increasing trends, while negative values indicate decreasing trends. The coefficient of determination, R2, measures how much the temperature variability is attributable to the time period. Usually, if the residuals are independent and normally distributed around zero, a classical hypothesis test assesses a significant trend if the null hypothesis, β=0, is rejected at the 0.05 level (Wooldridge, 2015). A widespread method to compute an estimate of β is the ordinary least-squares (OLS) procedure. However, this method has a twofold drawback. First, the hypothesis of the normal distribution of residuals needs to be validated. Secondly, a single outlier can have a significant effect on the estimation to the point of invalidating the trend interpretation (Rousseeuw, 1984).
On the other hand, the effect of outliers is tolerated by the robust regression3, which allows for a different distribution of residuals (Rousseeuw and Yohai, 1984). In the dataset considered here, the hypothesis of normal distribution is also sometimes violated due to the presence of outliers (see Fig. 2). Therefore, a robust regression procedure was applied to assess the temperature trends of the 32 stations. As before, a p value of less than 0.05 assesses that an estimated slope β is significantly different from zero. There are various methods to estimate the slope robustly. In this paper, the estimation was carried out using the so-called S estimator. Suppose is the sample dataset. Let ρ be a symmetric, continuously differentiable function with such that ρ is strictly increasing in [0,c] and is constant in with c being a suitable positive constant. Suppose f(x) is the standard normal probability density function and set The S estimator of β is
with and being the solution of
The results obtained from the previous methods have been further verified using the MK test and Sen's slope estimator method. The MK test is one of the most widely used nonparametric methods to detect trends in time series, with applications in different fields of research such as hydrology and climatology (Radhakrishnan et al., 2017). The magnitude of the trend is usually measured by Sen's slope estimator (Bhuyan et al., 2018; Radhakrishnan et al., 2017). Both of these nonparametric methods might be appropriately used for non-normally distributed censored time series including missing values. In the MK test4, the following assumptions hold: (i) in the absence of a trend, observations are independent and identically distributed; that is, the observations are not serially correlated over time. (ii) Observations are representative of actual conditions at the time of sampling; (iii) sample collection, management, and measurement methods provide unbiased and representative observations of underlying populations over time. Therefore, for the two-sided test, the zero hypothesis is that the time series has no monotonic trend. If N is the sample size, the MK test statistic is calculated according to Mann (1945):
where sgn is an indicator function taking values of −1, 1, or 0 according to its negative, positive, or equal-to-0 (tie) argument. Thus, the MK statistic returns the sum of the number of positive differences with the number of negative differences subtracted for all the considered differences. Note that E[S]=0 and that the variance including the correction term for ties is
where n is the number of tied groups and tk is the size of the kth tied group. The statistic S is approximately normally distributed, with a score of
If the p value of the test is below an appropriate significance level (0.05 and 0.01), then there is statistically significant evidence of the presence of a trend in the time series data. Before applying the MK test, the data were tested for serial correlation, which can severely affect the results and confirmed that there was no serial correlation in the annual and monthly mean temperature. Indeed, positive auto-correlation among the data would increase the chances of rejecting the null hypothesis even if there is the absence of a trend (Cox and Stuart, 1955).
The magnitude of the trend is estimated with the help of Sen's slope estimator5 (Bhuyan et al., 2018). The null hypothesis indicates no trend in the time series against a two-sided alternative. Indeed, first, the slope Ti of all data pairs is computed as follows:
Sen's slope estimator is then calculated as the median of all slopes; that is, the following applies:
Positive values of Q indicate an upward or increasing trend, whereas negative values indicate a downward or decreasing trend.
In this study, nonparametric methods were used because data from some stations have non-normal distributions (see Table 2 ). As discussed in Sect. 3.1, this hypothesis fails due to the presence of outliers. Therefore, we took the opportunity to assess how much the presence of outliers might influence significant trends. This assessment was done by applying all the previously described methods regardless of the assumption of normal distributions and discussing a posteriori (see Sect. 3) the slopes of the trends and their coefficients of determination.
2.2.2 Hierarchical clustering with dynamic time warping
This section summarizes the dynamic time warping (DTW) procedure for determining the distance matrix between any two-time series and shows how hierarchical clustering is used to find clusters exhibiting unique patterns of behavior.
A warping path, W, is an alignment between two sequences, and also with n≠m, entailing a one-to-many mapping for every pair of elements. Thus, the DTW procedure is a distance measure used to measure the similarity between two time series by finding the optimal warping path between them. To this aim, a distance measure is used; that is, DTW looks for the optimal alignment minimizing the distance between corresponding points (Shen and Chi, 2017).
The algorithm firstly constructs a cost matrix, C, where each element C(i,j) represents the cost of the pair (xi,yj) determined by utilizing a distance function, such as the Manhattan distance, , or the Euclidean distance, , between two points of the time series. The Manhattan distance was chosen because it is more robust in the presence of outliers in the data, and most of the stations examined have outliers, as shown in Fig. 2. In contrast, the Euclidean distance amplifies the effect of outliers by squaring their differences. Additionally, the Manhattan distance is preferred over the Euclidean distance with high-size samples. Then, a second matrix, DTW, is set up with the same dimension of the cost matrix. Its (i,j)th element gives the distance between two sub-sequences, and . Matrix DTW is initialized as follows: DTW as the distance between two empty sequences is 0, or DTW DTW for , and i≠j as no direct alignment is possible. The cost matrix values are then calculated recursively, taking into account the following constraints on the warping paths:
- (a)
the alignment starts at pair (1,1) and ends at pair
- (b)
the order of the elements in X and Y's path should be maintained constant;
- (c)
a pair (xi,yj) can be followed by the three possible pairs , and
The recursive functions corresponding to the three possible moves are
where wh, wv, and wd are the weights for the horizontal, vertical, and diagonal move. When all weights are equal, i.e., , the recursive function facilitates diagonal alignment because the cost of one step is lower than the cost of two steps combining the vertical and horizontal alignments. One way to balance this bias is to choose weights of .
The final DTW distance6 is the total cost of the optimal warping path, which measures how well the two sequences can be aligned while minimizing the overall cost. Smaller DTW distances indicate greater similarity between the sequences as they require less distortion to align optimally. DTW is susceptible to overfitting, which can occur, for example, if the warping window is not chosen appropriately in sequences of equal length, leading to inflated similarity scores between sequences. To overcome this drawback, a regularization technique can be introduced by adding a penalty term to the cost function, aiming to penalize excessive or large warping steps. This penalty term can be added to the original DTW cost function as follows: , where λ is the regularization parameter, tuning the strength of the regularization, and γ(i,j) is the regularization term. We have set With this choice, alignment steps that have a large difference in indices are penalized, discouraging the alignment from jumping too far off the diagonal.
Hierarchical clustering (HCA) is an algorithm for grouping similar objects into groups called clusters. The distances between these objects are initially given by the regularized DTW distance matrix. The output is a set of clusters, where every cluster has different characteristics from others and the objects within it are broadly similar to one another. The algorithm7 initially splits the sample into clusters, each containing only one sample point. A proximity matrix, D, is initialized as and The two clusters with a smaller proximity index are then merged in a new cluster called, for example, Cnew. After merging, the proximity matrix, D, is updated by recalculating the proximity index between the newly formed cluster, Cnew, and the remaining cluster, Ck, using the complete linkage criterion. This criterion picks the two farthest (most dissimilar) points such that one point lies in one cluster and the other point lies in a different cluster and defines the proximity index between these two clusters as the maximum regularized DTW between these two data points. The procedure continues by identifying the next pair of clusters with the smallest proximity index, merging them, and updating the matrix, D, still using the complete linkage criterion. This procedure is repeated until all clusters are merged into one or until the desired number of clusters is obtained. The final output is a hierarchical tree (dendrogram) that shows the sequence of merges and the distances at which each merge occurred. Although a classical way to analyze the result of HCA is to use the dendrogram, we chose a table representation (Tables 5 and 6 for monthly mean air temperatures and their slopes, respectively) to highlight which stations deviate from the geographic group they belong to. Tables 5 and 6 show the analysis for four clusters that correspond to the four geographic areas considered. A sensitivity analysis was performed (Table 4) that confirms the choice of the four clusters as the optimal choice.
Clustering performance with a given number of clusters was measured using the silhouette score (Rousseeuw, 1987). This index measures how similar a data point is to its cluster compared to other clusters. For this purpose, the mean intra-cluster distance, a, is compared with the mean nearest-cluster distance, b, for each data point. In detail, the mean distance between the ith data point, xi, in CI and all other data points in the same cluster (CI) is defined as follows:
where is the cardinality of the cluster and d(i,j) is the distance between xi and xj in cluster CI. The normalization is done with respect to as distance d(i,i) is not included in the sum. Therefore, the smaller the value a(i), the better the assignment of xi to CI. Similarly, the mean dissimilarity, d(i,Cj), of xi to some other cluster CJ≠CI is defined as the mean of the distance between xi and each xj∈CJ; that is, the following applies:
The minimum of these dissimilarity indexes identifies the “neighboring cluster” of xi because it is the next-best-fit cluster for point xi. Thus, the silhouette score8 corresponding to xi is defined as follows:
An overall silhouette score, S, is computed by taking the mean of all S(i) values. As for all data points, the same happens for S ranging from −1 to 1. Hence, a value of S close to 1 suggests that the data points are well clustered, and each one is more similar to a neighboring point in its own cluster as opposed to those within another cluster. A value of S of about 0 indicates that data points are located at or near the boundary between clusters. A negative value of S is likely to suggest that data points may be better allocated in a neighboring cluster rather than their current cluster.
Distance correlation (Székely and Rizzo, 2009) is a dependency measure used to examine and quantify relationships between the temperature data collected for the 32 stations. Distance correlation is invariant to not only linear transformations but also some nonlinear transformations and, unlike traditional methods, does not require assumptions of normality. As with other correlation measures, distance correlation ranges from 0 to 1, where 0 means no correlation and 1 means perfect correlation. For the calculation of the distance correlation9, suppose we have a random sample, , of n random vectors i.i.d to (X,Y) of dimension p and q, respectively. First, for , the Euclidean distance is computed between different samples as follows:
with denoting the Euclidean distance. Then, the following is defined:
where
and a similar set of steps for , and is performed. These values are then used to compute the distance covariance (dcov) using
and the distance correlation (dcor) by
where and
In the following, annual and monthly trends are explored using the parametric and nonparametric methods outlined in Sect. 2.2. Hierarchical clustering, as described in Sect. 2.2.2, is employed to discover the similarity between monthly mean temperature patterns within and between groups of stations. The distance matrix in each month for the 32 stations is used to find where the correlations are significant.
3.1 Annual average temperature trends
To get the annual temperatures, an averaging transformation over each year was applied, grouping half-hourly and hourly measurements into the monthly and annual time windows. For each station, box plots of the annual mean temperature time series are depicted in Fig. 2. The difference between the colder highlands (black, cyan, and blue) and the warmer lowlands (orange, yellow, and magenta) is evident as well as that between the colder UK stations (blue and magenta) with respect to the warmer Italian stations. In each group, some of the stations exhibit outliers, potentially affecting the hypothesis of normal distribution. Indeed, a single outlier can have a substantial effect on the trends obtained by the OLS method (Rousseeuw, 1984). Thus, to assess this hypothesis, the Shapiro–Wilk test was applied for each station. The results of the Shapiro–Wilk test are shown in Table 2. The test rejects the null hypothesis for the stations Valpelline, Aonach Mòr, Costigliole, and all UK lowland stations. As the box plot in Fig. 2 shows, all these stations have outliers. In particular, Valpelline and all UK lowland stations exhibit a single lower outlier. Once this outlier is removed, the Shapiro–Wilk test no longer rejects the hypothesis of a normal distribution. It is worth noting that these outliers correspond to the year 2010, which was the coldest year due to the co-presence of two very cold winter months – January and December10. This analysis highlights the significant impact of outliers causing non-normal distribution.
Table 2p values of the Shapiro–Wilk test for normal distribution. Stations marked in bold and with an asterisk (*) denote statistically significant trends at the 5 % significance level.
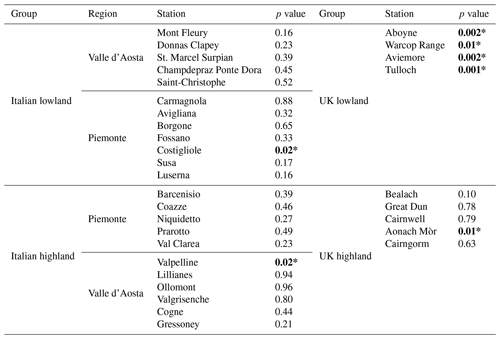
The normal distribution hypothesis is not rejected for all Italian highland stations except Valpelline. It is worth mentioning that the Valpelline station is located at the lowest altitude among the Italian Valle d'Aosta highland stations. Italian lowland stations show a comparable median that is fairly symmetrical concerning dispersion. The only exception is the Costigliole station, for which data are not normally distributed. Outliers at stations in the UK highlands do not affect the distribution of annual mean temperature except in the case of the Aonach Mòr station. According to the results of the Shapiro–Wilk test for the UK lowland stations, their annual mean temperature showed a deviation from the normal distribution. The effect of this result on the annual mean temperature trend test is examined later on.
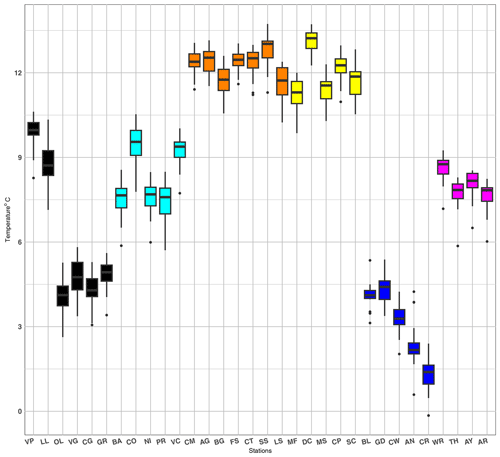
Figure 2Box plots of the annual average temperatures of all stations: black and cyan box plots represent Valle d'Aosta and Piemonte in the Italian highlands. Orange and yellow box plots correspond to Piemonte and Valle d'Aosta in the Italian lowlands, respectively, while blue and magenta box plots represent the UK highland and lowland stations.
Table 3 shows the results of the methods outlined in Sect. 2.2.1 to compute trends in annual mean temperatures. The fourth and fifth columns refer to the OLS method and the S estimator, respectively. Their slopes and R2 coefficients of determination are given in each subcolumn. The sixth column refers to the MK test and Sen's slope estimator. The subcolumns report p values, Sen's slope estimators, and R2 coefficients of determination, respectively.
Table 3Parametric and nonparametric methods of Sect. 2.2 applied to the average annual temperatures. Stations marked in bold and with an asterisk (*) denote statistically significant trends at the 5 % significance level. The unit of slopes is °C yr−1.
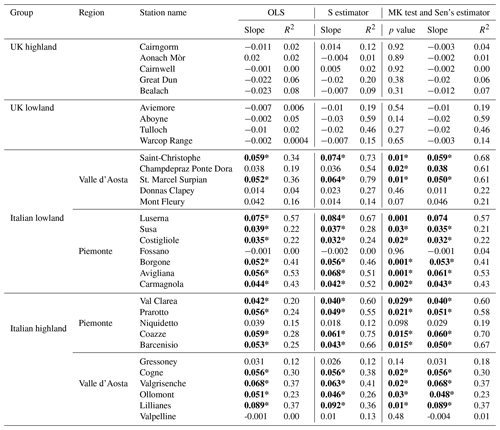
In the Italian highland group, most stations exhibit a significant positive trend except for Valpelline, which shows a relatively small negative trend and also fails the normality test. The Gressoney and Niquidetto stations, on the other hand, show a nonsignificant positive trend in all methods, with varying degrees of fitting, depending on the method used. Similarly, most lowland stations in Italy show statistically significant positive slopes, with the exception of Fossano, which shows a nonsignificant negative trend in all methods. It is worth observing that the non-normality checked at the Costigliole station as well as the presence of outliers do not affect the statistical significance result of the three methods.
The stations in the UK highland exhibit statistically nonsignificant negative trends, with the exception of the Aonach Mòr, which shows a positive trend in the OLS and a statistically nonsignificant negative trend with the S estimator and Sen's estimator; this is because the OLS method reveals sensitivity to outliers and non-normality.
Lowland stations in the UK showed statistically nonsignificant negative trends; however, the robust regression and Sen's slope estimators produced slopes of similar magnitude relatively larger than those obtained by the OLS method. This result highlights the outlier tolerance and distribution independence of robust regression and Sen's slope trend analysis. It is noteworthy that the R2 value of the OLS method is smaller than the R2 values of the S estimator and Sen's estimator.
As anticipated, Table 3 shows how outliers and non-normal distribution affect trend analysis. For example, UK lowland stations with non-normal distributions (Shapiro–Wilk test; p<0.05) still have negative slopes in both parametric and nonparametric methods, indicating that outliers do not affect the trend but impact the coefficient of determination. OLS assigns a lower significance to trends compared to nonparametric methods. For normally distributed data, all methods detect significant trends except for Champdepraz, where Sen's slope found a statistically significant trend, while OLS and the S estimator did not. These findings confirm that Sen’s slope estimator method with the MK test is the better method for trend analysis, with or without outliers.
These results are in agreement with those found in the French Alps and some adjacent regions of Italy and Switzerland (Durand et al., 2009), where it was observed that in spite of the fluctuations in the trend varying by altitude, season, and region, there is a general trend of increasing average annual temperatures. Similar studies conducted in Spain (El Kenawy et al., 2012), midwestern US, the Canadian prairies, western Arctic (Isaac and Van Wijngaarden, 2012), Croatia (Radhakrishnan et al., 2017), and India (Bhuyan et al., 2018) have reported a significant warming trend in average annual temperatures, indicating an overall increase over the past century. In addition, research carried out in Gombe State (Alhaji et al., 2018) showed a significant increase in maximum and average temperatures, while minimum temperature showed a nonsignificant upward trend. In Meshram et al. (2020), an increase in annual and seasonal temperatures between 1901 and 2016 is reported, focusing on Chhattisgarh. In contrast, highland and lowland stations in the UK showed nonsignificant cooling trends although the magnitude of the negative slope is smaller in absolute value.
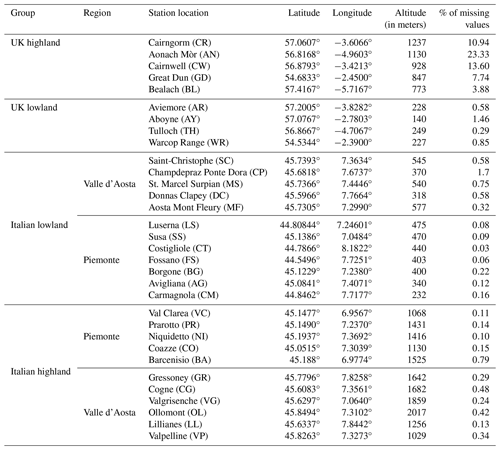
To assess the representativity of the considered 32 stations, their trends were compared with the average trends of the corresponding Italian and UK areas. Annual anomalies with respect to the average temperature values from 1991 to 2020 were then calculated. The National Oceanic and Atmospheric Administration (NOAA) algorithm (NOAA, 1987) was used for the two (one in Italy and one in the UK) geographic areas where the stations are included. They are about 4000 km2 in size, as defined by the coordinates 7°, 45° and −4°, 56°, respectively. The trend slopes were very similar to the average slopes reported in Table 3 at 0.0445°C yr−1 and −0.0047°C yr−1 for Italy and the UK, respectively. Therefore, the here considered 32 stations provide trend values consistent with those estimated over the corresponding wide areas where they are located (see Fig. 3).
3.2 Monthly temperature trends
The variability in monthly mean temperature trends at the 32 stations was assessed subsequently to an analysis of the annual mean temperatures. To get an initial descriptive overview of the characteristics shown by the stations for monthly mean temperature trends, the MK test and Sen's estimator were applied. In the following, we briefly summarize the results, highlighting similarities and differences.
Figure 4 represents the monthly mean temperature trends derived from Sen's slope estimator for the six distinct regions: the UK highland and lowland in the upper part, the Italian Valle d'Aosta region in the middle, and the Italian Piemonte region in the lower part of the figure. On the left are the highlands, while on the right are the lowland stations. Larger, bold data points highlight statistically significant warming and cooling trends.
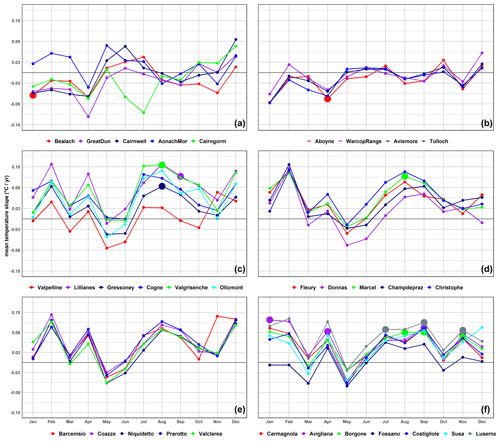
Figure 4The trends from Sen's slope estimators of monthly temperature time series from 2002 to 2021 at the UK stations (above) and Italian ones (in the middle are Valle d'Aosta stations and below Piemonte stations). On the left are highland stations, while on the right are the lowland ones. The larger dots represent the significant trends.
As shown in Fig. 4, both negative and positive trends occurred across the months. In the UK the slopes are generally lower than in Italy. For the UK, January to April show a decrease in temperature, while the Italian stations exhibit positive slopes for most of the months.
Going down into detail, the Italian stations generally displayed positive (warming) trends in summer, as well as in February, April, and December. In February, July, and August, the Italian highland stations recorded monthly temperature trends with values above 0.15 °C yr−1, while May and June showed values lower than −0.06 °C yr−1. Meanwhile, Italian lowland stations showed higher monthly temperature trends in January, February, April, July, August, and September raised above 0.06 °C yr−1 in most of the stations with the exception of Fossano, which showed negative trends in the first 3 months, different from other stations in its group, and lower values in March and May, falling below −0.06 °C yr−1. Specifically, the trends of all the stations in the Italian lowlands and highlands show a negative trend in May. Notably, the temperature patterns at the UK highland stations were different from those in the other two Italian groups but comparable to those in the UK lowlands (see Fig. 4). December stood out as the month with the highest trends at both highland and lowland stations in the UK. The temperature increased between 0.01 and 0.10 °C yr−1 in the highlands and between 0.01 and 0.06 °C yr−1 in the lowlands. The month of December in Italy also recorded generally quite high trends. Instead, stations in the UK behave in the opposite way to Italy in May, with an increase in trend values, while Italy shows a decrease everywhere. Another opposite behavior occurs in April, when all Italian stations showed an increasing trend, while in the UK, April is one of the months with the most significant decreasing trend, ranging between −0.04 and 0.12 °C yr−1.
Taking into account statistical significance, among the noteworthy results, there are two statistically significant cooling trends: one in January at the UK highland station Bealach and another in April at the UK lowland station Aboyne. Furthermore, statistically significant warming trends were observed in August for the Gressoney and Valgrisenche stations as well as in September and February for the Lillianes station. Saint Marcel, Avigliana, Borgone, and Luserna stations in the Italian lowland group displayed statistically significant warming trends in different months: Saint Marcel in August; Avigliana in January, April, September, and November; Borgone in August, September, and November; and Luserna in July, September, and November. Specifically, between September and November, three lowland Italian stations reported statistically significant warming trends; Avigliana exhibited the highest frequency of these warming trends.
Now we explore the resemblance of the temporal patterns of monthly mean temperature slopes (visible in Fig. 4) within and across the six groups. This analysis is a novelty in the literature of this field and relies on the hierarchical clustering technique in conjunction with regularized DTW. The results of hierarchical clustering for monthly mean temperatures are shown in Table 5: stations in each of the six groups of stations are assigned to one of the four clusters each month. The performance of this procedure is evaluated using the silhouette score, as shown in the final column of Table 5. The results of hierarchical clustering for the slopes of monthly mean air temperatures are shown in Table 6.
Prior to analyzing the monthly mean temperature and the slopes of monthly mean temperature hierarchical clustering within and across the groups, sensitivity analysis was examined as shown in Table 4 and determined the number of clusters. Four clusters are considered in this study. The choice of four clusters is mainly motivated by the results depicted in Table 4. Thus, the main goal is to test whether the observed data characterized the area to such an extent that they were found grouped in the same clusters. For completeness, a range from two to six was considered for the number of clusters, and the corresponding silhouette scores are shown in Table 4. In Table 4, specifying four clusters yields a higher overall mean silhouette score than the other settings. Reading Table 4 along the rows and comparing the scores for a given month across clusters, the four clusters have the highest silhouette score in the months from March to November. Based on this finding, together with the analysis of the geographical location of the stations and the shape of the dendrogram diagrams generated by hierarchical clustering, the optimal number of clusters in this study is four.
Table 4The silhouette scores of monthly mean temperature hierarchical clustering with a different number of clusters. The higher silhouette score over each row is highlighted in bold.
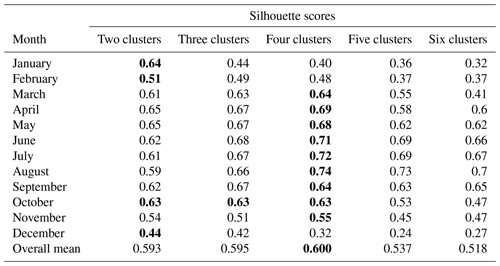
The hierarchical clustering is then implemented using four clusters. According to the experimental results of hierarchical clustering within a group, Italian highland stations are consistently classified into two clusters (Cluster I and Cluster II), while Italian lowland stations are consistently classified into Cluster IV in all months except January, November, and December (see the 10 stations clustered in Cluster I and Susa and Donnas Clapey clustered in Cluster III in January, and in December, four stations, Carmagnola, Marcel Surpian, Aosta Mont Fleury, and Saint-Christophe are clustered in Cluster I). UK lowland stations are classified in the same cluster for all months; however, their cluster assignments differ due to the similarity measure across the six groups. UK lowland stations are grouped into three clusters: Cluster I spans from March to May and September to November, Cluster II spans from June to August, and Cluster IV spans from December to February. UK highland stations are consistently classified into the same cluster in seven different months and inconsistently clustered in the other five months.
The Italian highland's Valpelline, Lillianes, Coazze, and Val Clarea stations at 1029, 1256, 1130, and 1068 m, respectively, were identified in the same clusters for every month, suggesting comparable patterns in monthly mean temperatures. The other four Italian highland stations, Gressoney at 1642 m, Ollomont at 2017 m, Valgrisenche at 1859 m, and Cogne at 1682 m, are likewise grouped into a unique cluster as they show a similar monthly mean temperature pattern. Consequently, the Italian highland stations are organized into two clusters except in January and November, reflecting similarities in monthly average temperature patterns (see also Table 5). This clustering is confirmed by the silhouette score in a range from 0.32 in December to 0.74 in August.
All the stations situated in the Italian lowland – Avigliana at 340 m, Borgone at 400 m, Carmagnola at 232 m, Luserna at 475 m, Susa at 470 m, Costigliole at 440 m, Fossano at 403 m, Aosta Mont Fleury at 577 m, Donnas Clapey at 318 m, Marcel Surpian at 540 m, Champdepraz Ponte Dora at 370 m, and Saint-Christopher at 545 m – are consistently clustered together. These stations were assigned to Cluster IV for nine months, with silhouette scores ranging from 0.48 to 0.74, and to Clusters I and IV in the remaining months, with silhouette scores of 0.55 and 0.40, respectively. The only exception was the Susa and Donnas Clapey stations which were always assigned to the same cluster. Susa and Donnas Clapey stations are grouped in Cluster III with no intra- and inter-cluster with other stations in December.
Considering the UK highland, most months showed a silhouette score between 0.64 and 0.74, that is, a uniform clustering pattern among all stations. All stations are grouped in Cluster III. Among the UK highland stations, Great Dun and Bealach, are clustered in Cluster III in January and November and Cluster I in December, while Aonach Mòr and Cairngorm are clustered in Cluster III in October. In general, in the UK highlands, the monthly mean temperature showed uniform patterns in most months.
From the monthly mean temperature patterns across different groups, the UK lowland stations, the Italian lowland stations, and the UK highland stations have distinct clusters for every month, corresponding to distinct patterns. The four Italian highland stations are grouped consistently in Cluster II with the UK lowland stations in June, July, and August. They are also clustered with some stations of the UK highland stations in January, February, October, November, and December.
UK lowland stations showed a similar pattern to the Italian highland, with Valpelline, Lillianes, Val Clarea, and Coazze being consistently assigned to Cluster I and the other four stations assigned to Cluster II. In addition, the Valpelline, Lillianes, Val Clarea, and Coazze stations consistently show patterns similar to some of the Italian lowland stations in January, November, and December. Among all the stations, there is no consistent pattern shared between the Italian and UK highland stations. However, in some months, four of the Italian highland stations exhibited a pattern similar to that of the UK highland stations. Furthermore, the Italian lowland stations and the UK highland stations did not display consistent monthly mean temperature patterns for all months. Consequently, it can be concluded that monthly mean temperature patterns do not exhibit any persistent similarities between groups and that each group continues to exhibit its unique and stable monthly mean temperature features. However, UK lowlands and Italian highlands showed some sort of similarity in Cluster I and Cluster II for most months.
Table 5The classification of the 32 stations into four clusters using hierarchical clustering in conjunction with regularized DTW. The values of the silhouette score (S. score) are given in the last column.
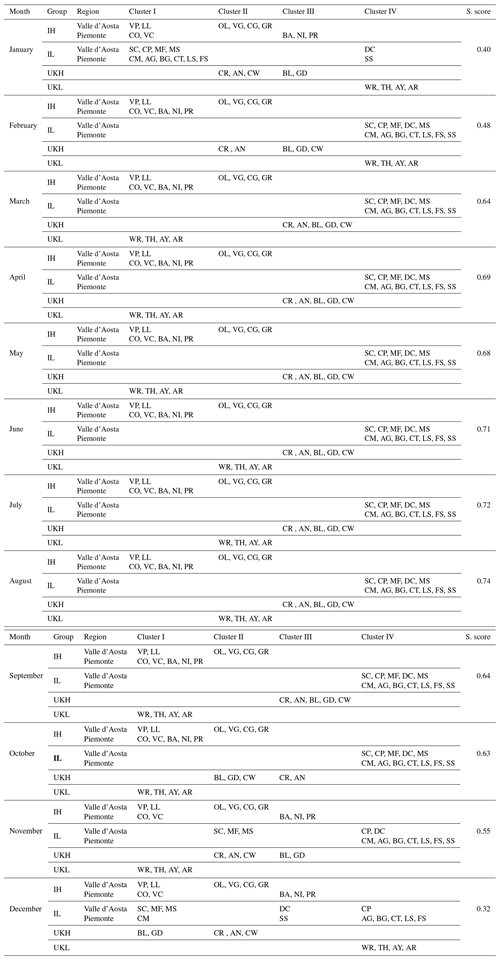
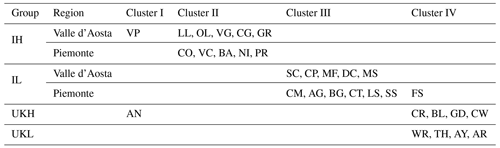
Table 6 shows the results of the hierarchical clustering with the DTW applied to the slopes of the monthly mean air temperature. Despite the obvious distinction between positive and negative slopes, Table 6 adds some further insights into understanding similarities/dissimilarities among stations although the estimated slopes are rather uncertain. Indeed, all of the stations in the UK highland and UK lowland are grouped into Cluster IV, with the exception of the Aonach Mòr station in the UK highland grouped into Cluster I. All of the Italian lowland stations are grouped into Cluster III. However, Fossano station is grouped in Cluster IV together with UK lowland and UK highland stations. The slope of the Italian highland station Valpelline is clustered in Cluster I together with the UK highland station Aonach Mòr, whereas the Italian lowland station Fossano is clustered together with the UK highland and the UK lowland stations in Cluster IV. These unusual behaviors with respect to the group they belong to can also be observed in Fig. 4. Indeed, Valpelline in the Italian highland, Fossano in the Italian lowland, and Aonach Mòr in the UK highland have distinct slope patterns within their reference groups. In particular, the slopes of the two Italian stations often trend lower than the lower slopes of their reference group. The opposite happens for the slope of Aonach Mòr. The fact that these two stations were grouped in Cluster I, thus showing different behaviors from all the others, may be due to the following reasons: Valpelline is the lowest of the mountain stations in Valle d'Aosta – and, in fact, its slopes in Fig. 4 are different from the others – while Aonach Mòr is missing 23 % of values. The Fossano station is the southernmost station in the entire Italian set and is beginning to have some sublittoral climatic effects. It is worth noting that this difference does not appear in the average data and thus in Table 5, but its trends in Fig. 4, especially in winter, are very different from those of the other stations. Other differences in the values of slopes related to specific months do not seem to affect the clustering. For example, the Cairngorm station showed a different pattern in two months (June and July). However, the hierarchical clustering tolerated this deviation and clustered Cairngorm along with its group. In conclusion, we can infer that the slopes of the UK highland and lowland stations are consistently grouped in Cluster IV, with the exception of Aonach Mòr. The slopes of Italian highland and lowland stations are grouped in Cluster II and Cluster III, respectively, with the exception of Valpelline and Fossano.
Table 6The classification of the trends of the 32 stations into four clusters using hierarchical clustering in conjunction with DTW.
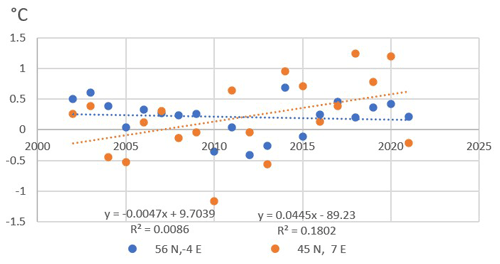
The distance correlation (see Fig. 5a) of the 32 stations is employed to quantify the strength of relationships of the trends of the monthly mean temperature. The stations in the highland of Piemonte showed a relatively strong correlation with the highland of Valle d'Aosta. We can see that the station has a relatively strong correlation within the six groups and a relatively weaker correlation between different groups, especially between Italian and UK stations.
Finally, the distance correlation matrix of the 32 stations in each month is presented in Fig. 5b. Interestingly, there was a strong correlation between every station and other stations in the same group. The Piemonte and Valle d'Aosta highland stations are highly correlated in the monthly mean temperature for every month (see Fig. 5b). It is also evident that the Italian highland and lowland stations are highly correlated in the monthly mean temperature for every month, with the exception of November and December. Most of the stations in the UK lowland and highland areas showed relatively strong correlations with each other in the monthly mean temperature for every month. However, the UK stations showed a weak correlation with the Italian stations, as depicted in Fig. 5b. In general, the Italian lowland stations exhibited a weaker correlation with the Italian highland stations in January, and, for some stations, this also occurred in November and December. Overall, the Italian highland and lowland stations show a stronger correlation. In comparison with Switzerland (Rebetez and Reinhard, 2008), the trends of Italian highland and lowland show less spreading in monthly trends, perhaps due to the fact that the Switzerland analysis was done in the period from 1975–2004. Also, Bruley et al. (2022) did not find a difference with altitude in monthly trends in the period from 1980 to 2015 in the Massif Central of France. Natural climate variability, however, poses inherent limits to climate predictability, which vary between areas with relatively lower or higher climate variability. The findings of our study can help to obtain a clearer picture of the time patterns, showing how they vary in different regions of Europe and at different altitudes. Understanding why the different months of the year behave in different way should require a more detailed study, but our results can provide the starting point for it, suggesting the employment of DTW and clustering to extend the analysis in many different areas of the world. For example, in the Mongolian Plateau between 1986 and 2004, an exceptional warming occurred, boosted by internal variability (Cai et al., 2024). In our results, the Italian highland trends are not enhanced with respect to lowland stations. Furthermore, Rogora et al. (2004) did not find a relation with the altitude in northwest Italian data, while Acquaotta et al. (2015) found it in the same Italian area. Indeed, even if all Italian stations in the present work show a general coherence of most monthly trends, in Fig. 4, a better correlation from November to February of mountain stations in both Italian areas is visible even if they are localized at about 70 km distance. On the map, it is easy to see Valle d'Aosta to the north and Borgone to the south. This result can also avoid doubts about the possible errors in measuring air temperature over snow, as proven by Huwald et al. (2009). In fact, the number of days with snow at the different stations can largely vary because of altitudes that are spread between 1000 and 2000 m a.s.l. Additionally, Salerno et al. (2023) recently found an unpredicted cooling in an area of high mountains in the Himalaya. The relevant warming trends in summer in the Italian stations can instead have important effects on the vegetation and carbon feedback (Zhang et al., 2022).
Regarding the possible causes of the monthly patterns, it is possible that the relatively lower warming of the UK is related to the decline in the strength of the Atlantic Meridional Overturning Circulation (AMOC) (Robson et al., 2016; Johnson and Lyman, 2020). For other insight, we refer to specific studies about the influence of dynamical drivers on monthly trends (Hoffmann and Spekat, 2021). Some hints for attributing trends to synoptic circulation are also in the literature, with specific references to European data (Fleig et al., 2015). It was the first attempt to understand the influence of global change on monthly trends. As a possible addition to this work, it could be interesting to compare cloud cover and sunshine trends with temperature trends. Some interesting work has been done in Italy by Manara et al. (2023).
In this paper, annual and monthly temperature trends of 32 stations of the Italian highland (five stations in Piemonte and six stations in Valle d'Aosta), Italian lowland (five stations in Valle d'Aosta and seven stations in Piemonte), UK highland (five stations), and UK lowland (four stations) were analyzed using the data collected from 2002 to 2021. The first purpose of the study is to analyze annual and monthly mean temperature trends. Furthermore, the unsupervised machine learning approach (hierarchical clustering in combination with DTW) is used to investigate the monthly mean air temperature patterns in order to measure the degree of similarity within and between the six groups of stations. The silhouette score is used to assess how effectively the clustering procedure performs. The main novelty of the paper is showing that stations with similar locations and altitudes have similar monthly slopes by quantifying them using DTW and clustering methods. These results reveal the nonrandomness of different trends throughout the year and between different parts of Europe, with a modest influence of altitude in wintertime. Two different regions of Europe were chosen because of the different climate and temperature trends – namely, northern UK (smaller trends) and northwest Italian Alps (greater trends).
The results of this study indicated a general warming trend in annual mean air temperature, with statistically significant warming observed at 8 of the 11 stations of the Italian highland and 9 of the 12 stations in the Italian lowland. Nonsignificant decreasing trends are detected at Valpelline in the Italian highland group as well as at Fossano in the Italian lowland group. Conversely, the mean annual air temperature in the UK highland and the UK lowland at all stations showed a statistically nonsignificant cooling trend. At most stations, the results obtained from the parametric and nonparametric methods used in this study are comparable. The bias of distribution and data outliers in the OLS method are evident at some stations, particularly those that differ from normal ones, such as Valpelline and Aonach Mòr. Due to the non-normal nature of the annual mean air temperature at Valpelline, Costigliole, Aonach Mòr, and all stations in the UK lowland, differences in the magnitude of slopes and R2 values are seen among the UK lowland stations when comparing the OLS and other methods. Nevertheless, all methods indicate a nonsignificant cooling trend across all UK stations.
Analyzing trends in monthly average air temperature, negative slopes were observed in May and June at most Italian stations, indicating a cooling trend. The months of February, August, and December, on the other hand, demonstrated clear warming trends. In the Italian highlands, the Valpelline station is an exception, with a decreasing trend in March, October, and November. Compared with Italian stations, the UK highland and lowland stations generally have more months with cooling trends.
Hierarchical clustering showed that stations within the same group had similar monthly mean temperature patterns. The similarity which can be seen in Fig. 4 has been justified with clustering and correlation methods, as also shown in Fig. 5. As an exception, the Italian highland stations are grouped into two clusters: Valpelline, Lillianes, Coazze, and Val Clarea are grouped in one cluster and the other four (Ollomont, Valgrisenche, Gressoney, and Cogne) stations are grouped in another cluster for all months. The peculiarities of Valpelline, Fossano, and Aonoch Mòr can be attributed, respectively, to the fact that Valpelline is the lowest in elevation of its group; Fossano is the most southern of the Italian ones, with some sublittoral influence; and Aonoch Mòr has a large number of missing values. It would be reasonable to increase the number of clusters by increasing the number of involved geographic areas: for example, by adding midland areas. This is no doubt a possible subject of future research.
The main result of the paper is clearly showing the different time patterns in each month for each group of stations. This was also done using the distance correlation matrix that shows strong correlations among the Piemonte and Valle d'Aosta highland stations every month. This pattern is also evident for most of the UK highland and lowland stations. These results are in agreement with the geographic location of the stations and are not too surprising. Considering a finer temporal scale, such as daily mean temperatures, would be useful for a more comprehensive analysis of the dependence. This analysis is in progress and will be the subject of future studies. Actually, stratifying monthly temperatures already allow us to add some non-obvious observations about correlations between stations. The Italian highland and lowland stations show a higher correlation every month with the exception of January, November, and December. Hence, the Italian lowland stations show a weaker correlation with the Italian highland stations in those three months. The distance correlation matrix depicts weak correlations among the UK and Italian stations.
Whatever their correlation, the processes underlying the various combined processes that cause these monthly and annual trends are beyond the scope of this paper. The findings of the present paper enhance the need to understand the temperature dynamics in the different groups and altitudes of Europe. These results also emphasize the importance of continuous monitoring and analysis of data in order to better quantify climate change.
Temperature data are freely available from Met Office, Corpo Forestale della Valle d’Aosta (CFVDA), and Agenzia Regionale per la Protezione Ambientale del Piemonte (ARPA Piemonte). The results of this paper are available upon request from the authors. The code is available at https://doi.org/10.5281/zenodo.14070482 (Liyew, 2024).
The authors confirm contribution to the paper as follows. Study conception and design: CML, EDN, RM, and SF; data curation: SF and CML; software: CML; methodology: CML and EDN; analysis and interpretation of results: CML, SF, and EDN; manuscript draft preparation: CML, EDN, and SF; review and editing: CML, EDN, RM, and SF; financial sourcing: SF. All authors read and approved the final version of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors would like to acknowledge the MUR (Ministry of University and Research) for financial support (see subsequent section). We extend our heartfelt appreciation to the diligent efforts of the reviewers and the guidance of the chief editor, whose invaluable contributions have significantly enriched the quality and depth of this paper.
This research has been supported by the NODES project, which has received funding from MUR – M4C2 1.5 of the National Recovery and Resilience Plan (PNRR) funded by the European Union NextGenerationEU program (grant no. ECS00000036). It was also partially funded by the Progetti di Ricerca di Interesse Nazionale (PRIN) 2022 project “Snow Droughts Prediction in the Alps: A Changing Climate”.
This paper was edited by Seung-Ki Min and reviewed by two anonymous referees.
Acquaotta, F., Fratianni, S., and Garzena, D.: Temperature changes in the North-Western Italian Alps from 1961 to 2010, Theor. Appl. Climatol., 122, 619–634, https://doi.org/10.1007/s00704-014-1316-7, 2015. a
Alhaji, U., Yusuf, A. S., Edet, C. O., Oche, C., and Agbo, E. P.: Trend analysis of temperature in Gombe state using Mann Kendall trend test, J. Sci. Res. Rep., 20, 1–9, https://doi.org/10.9734/JSRR/2018/42029, 2018. a
Bhuyan, M. D. I., Islam, M. M., and Bhuiyan, M. E. K.: A trend analysis of temperature and rainfall to predict climate change for northwestern region of Bangladesh, Am. J. Clim. Change, 7, 115–134, https://doi.org/10.4236/ajcc.2018.72009, 2018. a, b, c
Blackport, R., Fyfe, J. C., and Screen, J. A.: Decreasing subseasonal temperature variability in the northern extratropics attributed to human influence, Nat. Geosci., 14, 719–723, 2021. a
Bruley, E., Mouillot, F., Lauvaux, T., and Rambal, S.: Enhanced spring warming in a Mediterranean mountain by atmospheric circulation, Sci. Rep., 12, 7721, https://doi.org/10.1038/s41598-022-11837-x, 2022. a
Brunetti, M., Maugeri, M., Monti, F., and Nanni, T.: Temperature and precipitation variability In Italy in the last two centuries from homogenised instrumental time series, Int. J. Climatol., 26, 345–381, 2006. a
Byrne, M. P., Boos, W. R., and Hu, S.: Elevation-dependent warming: observations, models, and energetic mechanisms, Weather Clim. Dynam., 5, 763–777, https://doi.org/10.5194/wcd-5-763-2024, 2024. a
Cai, Q., Chen, W., Chen, S., Xie, S.-P., Piao, J., Ma, T., and Lan, X.: Recent pronounced warming on the Mongolian Plateau boosted by internal climate variability, Nat. Geosci., 17, 181–188, https://doi.org/10.1038/s41561-024-01377-6, 2024. a
Collins, M., Knutti, R., Arblaster, J., Dufresne, J. L., Fichefet, T., Friedlingstein, P., Gao, X., Gutowski, W. J., Johns, T., Krinner, G., Shongwe, M., Tebaldi, C., Weaver, A. J., and Wehner, M.: Long-term Climate Change: Projections, Commitments and Irreversibility, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a
Cox, D. R. and Stuart, A.: Some quick sign tests for trend in location and dispersion, Biometrika, 42, 80–95, https://doi.org/10.2307/2333424, 1955. a
Di Bernardino, A., Iannarelli, A. M., Diémoz, H., Casadio, S., Cacciani, M., and Siani, A. M.: Analysis of two-decade meteorological and air quality trends in Rome (Italy), Theor. Appl. Climatol., 149, 291–307, https://doi.org/10.1007/s00704-022-04047-y, 2022. a, b
Durand, Y., Laternser, M., Giraud, G., Etchevers, P., Lesaffre, B., and Mérindol, L.: Reanalysis of 44 yr of climate in the French Alps (1958–2002): methodology, model validation, climatology, and trends for air temperature and precipitation, J. Appl. Meteorol. Climatol., 48, 429–449, https://doi.org/10.1175/2008JAMC1808.1, 2009. a, b
El Kenawy, A., López-Moreno, J. I., and Vicente-Serrano, S. M.: Trend and variability of surface air temperature in northeastern Spain (1920–2006): linkage to atmospheric circulation, Atmos. Res., 106, 159–180, https://doi.org/10.1016/j.atmosres.2011.12.006, 2012. a, b, c
Farooq, I., Shah, A. R., Salik, K. M., and Ismail, M.: Annual, seasonal and monthly trend analysis of temperature in Kazakhstan during 1970–2017 using non-parametric statistical methods and GIS technologies, Earth Syst. Environ., 5, 575–595, https://doi.org/10.1007/s41748-021-00244-3, 2021. a, b
Fleig, A. K., Tallaksen, L. M., James, P., Hisdal, H., and Stahl, K.: Attribution of European precipitation and temperature trends to changes in synoptic circulation, Hydrol. Earth Syst. Sci., 19, 3093–3107, https://doi.org/10.5194/hess-19-3093-2015, 2015. a
Gil-Alaña, L. A., Gupta, R., Sauci, L., and Carmona-González, N.: Temperature and precipitation in the US states: long memory, persistence, and time trend, Theor. Appl. Climatol., 150, 1731–1744, https://doi.org/10.1007/s00704-022-04232-z, 2022. a
Giorgino, T.: Computing and visualizing dynamic time warping alignments in R: the dtw package, J. Stat. Softw., 31, 1–24, 2009. a
Hoffmann, P. and Spekat, A.: Identification of possible dynamical drivers for long-term changes in temperature and rainfall patterns over Europe, Theor. Appl. Climatol., 143, 177–191, https://doi.org/10.1007/s00704-020-03373-3, 2021. a
Huwald, H., Higgins, C. W., Boldi, M. O., Bou‐ Zeid, E., Lehning, M., and Parlange, M. B.: Albedo effect on radiative errors in air temperature measurements, Water Resour. Res., 45, https://doi.org/10.1029/2008WR007600, 2009. a
Hyndman, R. J. and Athanasopoulos, G.: Forecasting: principles and practice, OTEXTS, Melbourne, Australia, 2018. a
Isaac, V. and Van Wijngaarden, W.: Surface water vapor pressure and temperature trends in North America during 1948–2010, J. Climate, 25, 3599–3609, https://doi.org/10.1175/JCLI-D-11-00003.1, 2012. a, b
Johnson, G. C. and Lyman, J. M.: Warming trends increasingly dominate global ocean, Nat. Clim. Change, 10, 757–761, https://doi.org/10.1038/s41558-020-0822-0, 2020. a
Khavse, R., Deshmukh, R., Manikandan, N., Chaudhary, J., and Kaushik, D.: Statistical analysis of temperature and rainfall trend in Raipur district of Chhattisgarh, Current World Environment, 10, 305–312, 2015. a
Li, Q., Sheng, B., Huang, J., Li, C., Song, Z., Chao, L., Sun, W., Yang, Y., Jiao, B., Guo, Z., Liao, L., Li, X., Sun, C., Li, W., Huang, B., Dong, W., and Jones, P.: Different climate response persistence causes warming trend unevenness at continental scales, Nat. Clim. Change, 12, 343–349, https://doi.org/10.1038/s41558-022-01313-9, 2022. a
Liyew, C. M.: cliyew/temperature_trends: Temperature Trends (temperature_trends), Zenodo [code], https://doi.org/10.5281/zenodo.14070482, 2024. a
Maechler, M., Rousseeuw, P., Croux, C., Todorov, V., Ruckstuhl, A., Salibian-Barrera, M., Verbeke, T., Koller, M., Conceicao, E. L. T., and Anna di Palma, M.: robustbase: Basic Robust Statistics, r package version 0.99-0, http://robustbase.r-forge.r-project.org/ (last access: 16 May 2023), 2023a. a
Maechler, M., Rousseeuw, P., Struyf, A., Hubert, M., and Hornik, K.: cluster: Cluster Analysis Basics and Extensions, r package version 2.1.5, https://CRAN.R-project.org/package=cluster (last access: 23 September 2023), 2023b. a
Manara, V., Brunetti, M., Wild, M., and Maugeri, M.: Variability and trends of the total cloud cover over Italy (1951–2018), Atmos. Res., 285, 106625, https://doi.org/10.1016/j.atmosres.2023.106625, 2023. a
Mann, H. B.: Nonparametric tests against trend, Econometrica, 13, 245–259, https://doi.org/10.2307/1907187, 1945. a
Meshram, S. G., Kahya, E., Meshram, C., Ghorbani, M. A., Ambade, B., and Mirabbasi, R.: Long-term temperature trend analysis associated with agriculture crops, Theor. Appl. Climatol., 140, 1139–1159, https://doi.org/10.1007/s00704-020-03137-z, 2020. a
Meyer, D. and Buchta, C.: proxy: Distance and Similarity Measures, r package version 0.4-27, https://cran.r-project.org/web/packages/proxy/index.html (last access: 23 September 2023), 2022. a
Mohsin, T. and Gough, W. A.: Trend analysis of long-term temperature time series in the Greater Toronto Area (GTA), Theor. Appl. Climatol., 101, 311–327, https://doi.org/10.1007/s00704-009-0214-x, 2010. a
Moritz, S. and Bartz-Beielstein, T.: imputeTS: Time Series Missing Value Imputation in R, The R Journal, 9, 207–218, https://doi.org/10.32614/RJ-2017-009, 2017. a
MRI: Elevation-dependent warming in mountain regions of the world, Nat. Clim. Change, 5, 424–430, https://doi.org/10.1038/nclimate2563, 2015. a
Mudelsee, M.: Trend analysis of climate time series: A review of methods, Earth-science reviews, 190, 310–322, https://doi.org/10.1016/j.earscirev.2018.12.005, 2019. a
NOAA: Climate at a Glance: Global Time Series, published November 2023, J. Comput. Appl. Math., 20, 53–65, 1987. a
Patterson, M.: North-West Europe hottest days are warming twice as fast as mean summer days, Geophys. Res. Lett., 50, 1–10, https://doi.org/10.1029/2023GL102757, 2023. a, b
Pohlert, T.: trend: Non-Parametric Trend Tests and Change-Point Detection, r package version 1.1.15, https://cran.r-project.org/web/packages/trend/index.html (last access: 23 May 2023), 2023. a, b
Radhakrishnan, K., Sivaraman, I., Jena, S. K., Sarkar, S., and Adhikari, S.: A climate trend analysis of temperature and rainfall in India, Clim. Change Environ. Sustain., 5, 146–153, https://doi.org/10.5958/2320-642X.2017.00014.X, 2017. a, b, c
Rebetez, M. and Reinhard, M.: Monthly air temperature trends in Switzerland 1901–2000 and 1975–2004, Theor. Appl. Climatol., 91, 27–34, https://doi.org/10.1007/s00704-007-0296-2, 2008. a, b
Rizzo, M. and Szekely, G.: energy: E-Statistics: Multivariate Inference via the Energy of Data, r package version 1.7-11, https://cran.r-project.org/web/packages/energy/index.html (last access: 1 October 2023), 2022. a
Robson, J., Ortega, P., and Sutton, R.: A reversal of climatic trends in the North Atlantic since 2005, Nat. Geosci., 9, 513–517, https://doi.org/10.1038/NGEO2727, 2016. a
Rogora, M., Arisci, S., and Mosello, R.: Recent trends of temperature and precipitation in alpine and subalpine areas in North Western Italy, Geogr. Fis. Dinam. Quat., 27, 151–158, 2004. a
Rousseeuw, P. and Yohai, V.: Robust regression by means of S-estimators, in: Robust and Nonlinear Time Series Analysis: Proceedings of a Workshop Organized by the Sonderforschungsbereich 123 “Stochastische Mathematische Modelle”, Heidelberg 1983, 256–272, Springer, https://doi.org/10.1007/978-1-4615-7821-5_15, 1984. a
Rousseeuw, P. J.: Least median of squares regression, J. Am. Stat. A., 79, 871–880, https://doi.org/10.2307/2288718, 1984. a, b
Rousseeuw, P. J.: Silhouettes: a graphical aid to the interpretation and validation of cluster analysis, J. Comput. Appl. Math., 20, 53–65, 1987. a
Royston, J. P.: An extension of Shapiro and Wilk's W test for normality to large samples, J. Roy. Stat. Soc. C, 31, 115–124, 1982. a
Salerno, F., Guyennon, N., Yang, K., Shaw, T. E., Lin, C., Colombo, N., Romano, E., Gruber, S., Bolch, T., Alessandri, A., Cristofanelli, P., Putero, D., Diolaiuti, G., Tartari, G., Verza, G., Thakuri, S., Balsamo, G., Miled, E. S., and Pellicciotti, F.: Local cooling and drying induced by Himalayan glaciers under global warming, Nat. Geosci., 16, 1120–1127, https://doi.org/10.1038/s41561-023-01331-y, 2023. a
Sardá-Espinosa, A.: Comparing time-series clustering algorithms in r using the dtwclust package, R package vignette, 12, 41, https://cran.radicaldevelop.com/web/packages/dtwclust/vignettes/dtwclust.pdf (last access: 18 September 2023), 2017. a
Sayemuzzaman, M., Mekonnen, A., and Jha, M. K.: Diurnal temperature range trend over North Carolina and the associated mechanisms, Atmos. Res., 160, 99–108, https://doi.org/10.1016/j.atmosres.2015.03.009, 2015. a, b
Shen, S. and Chi, M.: Clustering Student Sequential Trajectories Using Dynamic Time Warping., International Educational Data Mining Society, https://api.semanticscholar.org/CorpusID:19096679 (last access: 24 September 2023), 2017. a
Shen, X., Liu, B., Li, G., Wu, Z., Jin, Y., Yu, P., and Zhou, D.: Spatiotemporal change of diurnal temperature range and its relationship with sunshine duration and precipitation in China, J. Geophys. Res.-Atmos., 119, 13–163, https://doi.org/10.1002/2014JD022326, 2014. a
Shen, X., Liu, B., and Lu, X.: Weak cooling of cold extremes versus continued warming of hot extremes in China during the recent global surface warming hiatus, J. Geophys. Res.-Atmos., 123, 4073–4087, https://doi.org/10.1002/2017JD027819, 2018. a
Simmons, A., Hersbach, H., Munoz-Sabater, J., Nicolas, J., Vamborg, F., Berrisford, P., de Rosnay, P., Willett, K., and Woollen, J.: Low frequency variability and trends in surface air temperature and humidity from ERA5 and other datasets, ECMWF Technical Memoranda, 881, https://doi.org/10.21957/ly5vbtbfd, 2021. a
Székely, G. J. and Rizzo, M. L.: Brownian distance covariance, Ann. Appl. Stat., 3, 1236–1265, 2009. a
Tang, R., He, B., Chen, H. W., Chen, D., Chen, Y., Fu, Y. H., Yuan, W., Li, B., Li, Z., Guo, L., Hao, X., Sun, L., Liu, H., Sun, C., and Yang, Y.: Increasing terrestrial ecosystem carbon release in response to autumn cooling and warming, Nat. Clim. Change, 12, 380–385, https://doi.org/10.1038/s41558-022-01304-w, 2022. a
Twardosz, R., Walanus, A., and Guzik, I.: Warming in Europe: Recent trends in annual and seasonal temperatures, Pure Appl. Geophys., 178, 4021–4032, https://doi.org/10.1007/s00024-021-02860-6, 2021. a
Vinnikov, K. Y., Robock, A., and Basist, A.: Diurnal and seasonal cycles of trends of surface air temperature, J. Geophys. Res.-Atmos., 107, ACL 13-1–ACL 13-9, https://doi.org/10.1029/2001JD002007, 2002. a, b
Wooldridge, J. M.: Introductory econometrics: A modern approach, Cengage learning, 2015. a
Zhang, Y., Piao, S., Sun, Y., Rogers, B. M., Li, X., Lian, X., Liu, Z., Chen, A., and Peñuelas, J.: Future reversal of warming-enhanced vegetation productivity in the Northern Hemisphere, Nat. Clim. Change, 12, 581–586, https://doi.org/10.1038/s41558-022-01374-w, 2022. a
The function R na_seasplit() of the package imputeTS (version 0.3) was used to restore the missing information (Moritz and Bartz-Beielstein, 2017).
The R function lm() was used.
The R function lmrob() of the package robustbase (version 0.99-0) was used (Maechler et al., 2023a).
The R function proxy::dist() of the package proxy (version 0.4-27) was used (Meyer and Buchta, 2022). This distance is produced by the R function dtwDist of the package dtw (version 1.23-1) (Giorgino, 2009) and registered as a distance function in the database of distances pr_DB of proxy.
The R function hclust() was used. Equivalently, the R function tsclust() from the R package dtwclust can be used (Sardá-Espinosa, 2017).
The R function silhouette() was used from the package clusters (version 2.1.5) (Maechler et al., 2023b).
The R function dcor.test() of the package energy (version 1.7-11) was used (Rizzo and Szekely, 2022).
The coldest month of the seasonal cycle is usually either December or January.