the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Low-visibility forecasts for different flight planning horizons using tree-based boosting models
Sebastian J. Dietz
Philipp Kneringer
Georg J. Mayr
Achim Zeileis
Low-visibility conditions enforce special procedures that reduce the operational flight capacity at airports. Accurate and probabilistic forecasts of these capacity-reducing low-visibility procedure (lvp) states help the air traffic management in optimizing flight planning and regulation. In this paper, we investigate nowcasts, medium-range forecasts, and the predictability limit of the lvp states at Vienna International Airport. The forecasts are generated with boosting trees, which outperform persistence, climatology, direct output of numerical weather prediction (NWP) models, and ordered logistic regression. The boosting trees consist of an ensemble of decision trees grown iteratively on information from previous trees. Their input is observations at Vienna International Airport as well as output of a high resolution and an ensemble NWP model. Observations have the highest impact for nowcasts up to a lead time of +2 h. Afterwards, a mix of observations and NWP forecast variables generates the most accurate predictions. With lead times longer than +7 h, NWP output dominates until the predictability limit is reached at +12 d. For lead times longer than +2 d, output from an ensemble of NWP models improves the forecast more than using a deterministic but finer resolved NWP model. The most important predictors for lead times up to +18 h are observations of lvp and dew point depression as well as NWP dew point depression. At longer lead times, dew point depression and evaporation from the NWP models are most important.
- Article
(1419 KB) - Full-text XML
- BibTeX
- EndNote
Low-visibility conditions require special procedures to ensure flight safety at airports. These procedures slow down the air traffic and result in a reduction of the operational airport capacity, leading to mean economic loss for airports and airlines. In this study, we generate predictions of low visibility at thresholds that directly connect to the capacity-reducing procedures at Vienna International Airport. Accurate nowcasts of these low-visibility thresholds can help in reorganizing flight plans and reducing the economic losses. These forecasts, however, are not only important for flight plan reorganizations. They also have an impact on long-term flight planning to avoid expensive short-term reorganizations. This paper therefore focuses on nowcasts with lead times from +1 to +18 h and on medium-range forecasts with up to a +14 d lead time. Additionally, we are interested in the predictability limit, which is achieved when the improvement in the forecasts over the climatology vanishes.
Generally, low-visibility forecasts are generated with two different approaches (Gultepe et al., 2007). The first one is physical modeling and uses relevant physical equations to produce predictions in a defined model area. The second approach, statistical modeling, computes relations between the forecast variable and possible predictor variables from past data. Predictions are produced by applying the relationships to new data. An advantage of this approach is low computational cost and the possibility to directly forecast special quantities, such as visibility classes responsible for capacity reductions.
Statistically based visibility forecasts were investigated first by Bocchieri and Glahn (1972) using a multiple linear regression approach to forecast ceiling continuously and at several thresholds. The predictor variables of their forecasting model were the output of a numerical weather prediction (NWP) model. Based on this model approach, Vislocky and Fritsch (1997) produced forecasts of multiple binary thresholds of ceiling and visibility. By adding observations to the model predictors, they enhanced the performance at short lead times. This forecasting system was improved by Leyton and Fritsch (2003, 2004) by increasing the density and frequency of the surface observations. Ghirardelli and Glahn (2010) used multiple linear regression to generate an operational prediction system for several visibility and ceiling thresholds for multiple locations and lead times. A comparison of various statistical methods to forecast the same information as Ghirardelli and Glahn (2010), however in one combined variable, was conducted by Herman and Schumacher (2016). They compared K-nearest neighbor, gradient boosting, random forest, and support vector machine methods and found that no specific algorithm performs best overall. Further statistical methods used for visibility forecasts are decision trees (Dutta and Chaudhuri, 2015), Bayesian model averaging (Roquelaure et al., 2009), and neural networks (Marzban et al., 2007).
The operationally relevant visibility information for flight management is the low-visibility procedure (lvp) state, a combination of visibility and ceiling, which directly connects to capacity reductions at airports. It was forecasted first by Kneringer et al. (2019) and Dietz et al. (2019), who used ordered logistic regression and decision-tree-based models for observation-based nowcasts up to a +2 h lead time. Their forecasts are most relevant for short-term regulations. In order to conduct flight plan reorganizations, the air traffic management requires forecasts with lead times up to +18 h, and even longer forecasts are required for long-term flight planning. A scientifically interesting and yet unresolved question is when the predictability of lvp ends and the forecasts are no better than a climatological forecast.
The focus of this paper is therefore on determining the skill and most important model predictors for lvp nowcasts up to a lead time of +18 h and for medium-range forecasts from +1 d up to the – as of yet unknown – predictability limit. We generate forecasts with boosting trees, which Dietz et al. (2019) showed to perform the best at the shortest lead times, and compare their predictions to predictions of ordered logistic regression models, persistence, and climatology to analyze the benefits of the various models for lvp forecasts of different forecast horizons. The model predictors are based on current observations and output of NWP models and are valid for Vienna International Airport between September and March at 06:00 UTC. During this time, the lvp occurrence probability and the arrival rate are highest (Kneringer et al., 2019). The paper is organized as follows: Sect. 2 describes the data sources, the response, and the predictor variables used in this study. Afterwards, the statistical methods are explained and the results are analyzed and discussed.
Six years of data (November 2011–November 2017) are available to produce and evaluate forecasts, which result in 1177 observations when considering the cold season (October–March) at 06:00 UTC only. The forecasts are developed for one specific touchdown point at Vienna International Airport and consist of observations at Vienna International Airport and NWP model output. All observations used are measured close to the examined touchdown point.
The NWP model data used for forecast generation are from the atmospheric high-resolution (HRES) model and the ensemble prediction system (ENS) of the European Centre for Medium-Range Weather Forecasts (ECMWF). The HRES model provides forecasts with hourly output until a lead time of +90 h. Afterwards, the output is 3-hourly resolved until +144 h and 6-hourly resolved up to the maximum lead time of +240 h. This model is initialized daily at 00:00 and 12:00 UTC and provides one forecast for each lead time with a horizontal model resolution of in the latitude–longitude direction, conforming to grid boxes of approximately 9 km×9 km. During the training period the model was improved several times (changes in the horizontal and vertical model grid and the data assimilation scheme). A bilinear interpolation from the four closest grid points to the validation point, however, reduces the impact of model grid changes.
The ENS provides forecasts up to a +15 d (+360 h) lead time with 3-hourly output up to +144 h and 6-hourly output afterwards. Instead of only one forecast with each output, the ENS provides 50 forecasts (members) at each lead time. Each of the members is computed with slightly changed initial conditions, resulting in a different prediction. We use the mean and standard deviation of the ensemble as predictors for the models instead of information on all 50 members individually, which would result in an overly large, highly correlated predictor setup (Wilks and Hamill, 2007; Hamill et al., 2008; Herman and Schumacher, 2016). The ENS is initialized daily at 00:00 and 12:00 UTC on a global grid with a spatial resolution, conforming to grid boxes of approximately 18 km×18 km. Similarly to the HRES model, the ENS was improved several times during the model training period. The utilization of a bilinear interpolation again reduces the impact of model grid changes due to the output quality.
2.1 Forecast variable
The response is the lvp state, which is an ordered categorical variable that comes into effect when certain horizontal and/or vertical visibility thresholds are crossed at airports. The horizontal visibility thresholds are determined by observations of the runway visual range (rvr), defined as the distance over which the pilot of an aircraft on the centerline of the runway can see the runway surface markings or the lights delineating the runway or identifying its centerline (International Civil Aviation Organization, 2005). The vertical visibility thresholds are determined by ceiling (cei) observations. Ceiling is the base altitude of a cloud deck covering at least five okta of the sky.
The number of lvp states and their threshold values vary with the location, size, and technical equipment of the airport. Vienna International Airport has four different lvp states. Table 1 states their thresholds, related capacity reductions, and climatological occurrences. Since no restrictions (lvp0) occur in about 90 % of the cold season (October–March) and lvp2 is 4 times more frequent than the less restrictive state lvp1 and the maximum restrictive state lvp3, forecasts are challenging.
Table 1Definition of the lvp states with their thresholds in runway visual range (rvr) and ceiling (cei), their climatological occurrence probability, and their maximum operational capacity utilization for Vienna International Airport. The climatological occurrence probability is computed during the cold seasons (October–March) from November 2011 to November 2017 at 06:00 UTC.

2.2 Predictor variables
The model predictors consist of observations and output of NWP simulations. The observations used are the predictors that Kneringer et al. (2019) found as having the highest impact on nowcasts (see Table 2a). Horizontal visibility (vis) and rvr, which are both used as predictors, differ in the inclusion of background luminance and runway light quality, as well as the truncation at 2000 m for rvr (Federal Aviation Administration, 2006). Ceiling (cei) is postprocessed from ceilometer outputs (Dietz et al., 2019). The lvp state is computed by thresholds of cei and rvr as described in Sect. 2.1. The dew point depression (dpd) and temperature difference between 2 m and 5 cm a.g.l. (dts) are computed from temperature sensors in a close distance. The climatological information used as predictor is the solar zenith angle (sza) in order to capture the annual cycle.
The NWP model outputs used as predictors (Table 2b) are selected based on physical mechanisms of fog and cloud formulation and the results of Herman and Schumacher (2016). Each variable is internally derived by the ECMWF from the physical model equations using various physical and statistical relationships. Additionally, the dew point depression (dpdmodel) and temperature difference between 2 m and the surface (dtsmodel) are computed from the NWP model output 2 m temperature, dew point, and surface temperature.
Some of the statistical models use a combination of observations and NWP output as predictors. Observations are at points or along lines and as such have larger variability than grid values of NWP output. Also the NWP errors are larger due to model uncertainty and representation error (see Janjic et al., 2018). While observation and NWP representation error remain unchanged with forecast horizon, the increase in model error with an increasing forecasting time is handled by fitting separate statistical models for each forecast step.
Dietz et al. (2019) and Kneringer et al. (2019) considered tree-based models and parametric ordinal regression models to forecast low-visibility conditions with lead times up to +2 h. Here, the forecast horizon is pushed further out to +14 d by assessing and comparing the performance of tree-based models and parametric ordinal models as well as persistence and climatology. Special emphasis is given to boosting trees that Dietz et al. (2019) showed as performing best among other tree-based models and having comparable or slightly better performance than the ordinal models for the short lead times up to +2 h. The characteristics and properties of the models used for forecast generation and validation are described in the following.
3.1 Forecasting methods
To forecast the lvp state, we require models that are able to deal with ordered response variables. Ordered logistic regression (OLR), which projects the response by combining multiple linear features of the predictor variables, is a well-known statistical method for predicting ordered response variables. Another possibility is decision-tree-based ensemble modeling consisting of multiple merged decision trees. Decision-tree-based ensemble models allow interactions and – in contrast to the parametric OLR models – nonlinear effects.
3.1.1 Boosting trees
Tree-based boosting is an ensemble method that often achieves rather accurate forecasts based on relatively simple base learners. More specifically, the approach develops the final model iteratively by repeatedly fitting a base learner to the model gradients from the previous iteration. Typically, the base learner is a simple statistical model with low computational cost, such as decision trees.
Classical decision trees partition the predictor space into several regions, depending on the correlations between the response and the predictor variables, and fit a constant model to each terminal region. They are particularly appealing as base learners in boosting because they can naturally capture nonlinear patterns and interactions, handle predictors with different scales (continuous, ordinal, and nominal), and are invariant under monotone transformations of predictor variables (Bühlmann and Hothorn, 2007).
In this investigation, we employ the component-wise gradient boosting algorithm suggested by Bühlmann and Hothorn (2007) and extended by Schmid et al. (2011). The ordinal response variable lvp is modeled by the proportional odds model of Agresti (2003), and predictor variables are captured by the conditional inference trees of Hothorn et al. (2006) as base learners. In the case of lvp forecasts at Vienna International Airport, the proportional odds model is defined as
, where denotes the predictor variable vector with p predictors and observations. In the proportional odds model, the prediction function f=f(X) and the threshold values θk are estimated simultaneously (with θ3=∞).
To estimate the prediction function f* and the threshold values , the negative log likelihood of the proportional odds model is minimized over f and θ (shown in Appendix A). The boosting implementation of Schmid et al. (2011) for tree-based boosting of lvp states can be described as follows:
-
Set m=0 and initialize the prediction function by a decision tree and the threshold parameters , , and by offset values.
-
Increase m by 1 and compute the derivative of the log likelihood, . Evaluate at , and , leading to the gradient vector
-
Fit the gradient vector U[m] to the predictor variables by using a decision tree and set equal to the fitted values of the tree.
-
Update the predictor function , with as the shrinkage parameter for model growth.
-
Recompute the sum of the negative log likelihood with f(Xi) as and minimize it over θ. Set θ[m] equal to the estimated θ*.
-
Iterate steps 2–5 until a stopping criterion for m is reached.
The exact steps of the working algorithm are discussed separately by Bühlmann and Hothorn (2007) and Schmid et al. (2011). The main body of the algorithm is the iterative adding of the true gradient of the log likelihood to the current estimate of the predictor f*, leading to a continuous likelihood maximization of the boosting tree model. The stopping criterion for the algorithm is the number of maximum iterations m.
An additional benefit of boosting decision trees is the automatic selection of the predictors with the highest impact on the response, which is based on the automatic selection of split variables in the decision trees. Moreover, the number of terminal nodes can be used to specify the interactivity of the predictors in the trees. The combination of the additive structure of the boosting algorithm and the nonparametric structure of the trees makes boosting trees into a powerful alternative for predicting ordered response variables.
The described algorithm is implemented in the R package mboost (Hothorn et al., 2017). The number of trees for each model is determined by the minimized out-of-sample error. Therefore, the model score is computed for each iteration for up to a maximum number of 5000 iterations. The particular model for the iteration with the minimum score is then selected. The number of iterations differs for different training samples and for different lead times.
Reference models
The benefits of the boosting tree forecasts can be assessed by reference models. In this study, we apply several references, since their competitiveness changes with different lead time ranges.
Persistence
A widely used benchmark reference for short lead times is the persistence model (e.g., Vislocky and Fritsch, 1997), which assumes that the lvp state does not change between forecast initialization and validation. The persistence model predicts the current lvp state with a probability of 100 % and the remaining categories with 0 % for all lead times.
Climatology
At the long end of the forecast horizon, climatology is a competitive reference model. Climatology always predicts the distribution of the response in the training sample.
Ordered logistic regression (OLR)
For the comparison of the boosting tree performances to other statistical models, we use OLR, a well-known model for ordinal responses. Kneringer et al. (2019) developed an OLR model for lvp nowcasts with lead times up to +2 h that outperforms persistence, climatology, and predictions from human forecasters at Vienna International Airport. We support the OLR model with the same predictors as with the boosting trees. The predictions of OLR should be the most challenging ones for the boosting trees.
Direct model output
Another reference is direct output of the ECMWF NWP model, which has included visibility since May 2015 and ceiling since November 2016. Thus, the predicted lvp state can be computed directly from the NWP model output for one cold season (2016–2017). For the HRES model, only deterministic lvp state forecasts can be computed because the model consists of one member only. The ENS model, however, consists of 50 members, and therefore probabilistic forecasts can be derived by merging the predictions of all 50 members.
3.2 Model verification
The performance of probabilistic forecasts of ordered response variables, such as lvp, can be assessed by the ranked probability score (RPS; Epstein, 1969; Murphy, 1971; Wilks, 2011). The RPS of single forecast–observation pair i for lvp state predictions at Vienna International Airport is computed by the squared differences between the cumulative probabilities of the forecast and observation for each category:
where 𝟙(⋅) denotes the indicator function. The RPS notation used is normalized and yields an easier interpretation of the results, since the values of the normalized RPS are always between 0 and 1 instead of 0 and the number of response categories (the normalization factor of the RPS for lvp predictions at Vienna International Airport is 3 because of the four lvp categories). Lower RPS values indicate better performance.
To determine the performance of a particular model, all scores from the individual forecast–observation pairs are averaged. For comparison of the model score relative to a reference model, the ranked probability skill score (RPSS) is used:
The model RPS is computed out of sample by a season-wise cross-validation approach with error bootstrapping. The data set is divided into six blocks, each of which contains data from one cold season. Afterwards, the models are fitted on five blocks and validated on the remaining one until each block is used once for model validation.
Bootstrapping is used to assess model uncertainty. We generate 1000 data samples, each with randomly drawn out-of-sample scores from the six cross-validation blocks with replacement. The size of each sample is identical to the overall number of forecast–observation pairs. After bootstrapping, the mean RPS is computed for each sample. The distribution of these mean scores describes the model uncertainty.
3.3 Variable importance measurement
To provide useful information on the working process of the models and to determine their most important inputs, a variable importance measure is required. We use permutation accuracy importance, which Strobl et al. (2009) showed as being a reasonable measure for tree-based models. In permutation importance, the forecast performance of the original validation sample is computed and compared to the performance of the same validation sample, however with permuted values in one predictor variable (e.g., Breiman, 2001). To compute the permutation importance, the out-of-sample performance of the original validation sample is computed in the first step. After predictions from the original sample, one predictor variable of the original sample is permuted randomly, and new predictions – again with the same model – are generated from this modified sample. When permuting one predictor variable, the association with the response breaks and the prediction accuracy of the sample with the permuted predictor decreases. The stronger the decrease in forecast performance, the higher the impact of the permuted predictor. The loss in forecast performance is measured by the increase in the RPS. The procedure of permuting the values of one predictor variable and computing the performance of this modified sample is repeated for each predictor.
Moreover, to extract meaningful information on the most important predictors, permutation importance is conducted on each cross-validated sample. Afterwards, the results from the different samples are averaged to show the mean impact of each predictor on the forecast.
4.1 Nowcasts (+1 to +18 h)
This section is about lvp state forecasts with lead times from +1 to +18 h. The predictors for the statistical models are observations and output of the ECMWF HRES model – both separately and combined. The performances of the boosting trees with the different predictor setups are compared amongst others and to the references OLR, persistence, and climatology. Moreover, the predictors with the highest impact on the forecasts are examined and analyzed for their effects.
4.1.1 Model performance
The performance of the boosting trees with different predictor setups and the references persistence and climatology is given in Fig. 1a for the lead times +1 to +18 h. Boosting trees based on observations outperform persistence and climatology at each lead time. As expected, the difference in forecast performance between persistence and observation-based boosting tree predictions is smallest at the shortest lead times and increases with longer lead times. A longer distance between forecast initialization and validation leads to a higher probability of changing lvp states and therefore to a worsening of the persistence. Similarly, the relations of current observations and future lvp decrease with longer lead times and the observation-based models converge to climatology, however much slower than the persistence.
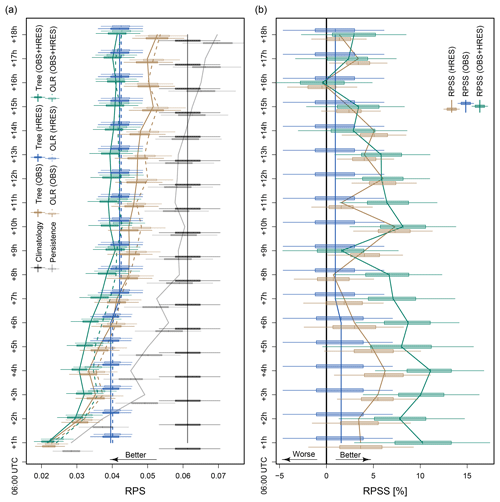
Figure 1Forecast performance of boosting tree models and the references OLR, persistence, and climatology. The statistical models are based on observations (OBS), NWP model output of the deterministic HRES ECMWF model (HRES), and their combination (OBS+HRES). The forecast validation time is always 06:00 UTC. Models with a lead time of +1 h (+2 h, …) are initialized at 05:00 UTC (04:00 UTC, …). The lines show the median performances, and the related boxes show the 25th to 75th percentiles with the 5th to 95th percentiles as whiskers. (a) RPS of each individual model. (b) RPSS of the boosting trees with OLR as reference. Boosting trees based on observations have the OLR based on observations as reference (the same applies for the HRES model and the combined predictor setup). The RPSS numbers show the percentage of improvement in the boosting tree performance over OLR.
The boosting trees based on the HRES output also outperform climatology up to a +18 h lead time. Their performance is constant for the lead times +1 to +6 h because of identical HRES information. In this investigation, we assume that NWP model output is available immediately after model initialization. The HRES model is initialized daily at 00:00 and 12:00 UTC. The closest output available for the 06:00 UTC forecast with a lead time of +1 h is from the 00:00 UTC initialization with a lead time of +6 h. This information is used for the lead times from +1 to +6 h. The same applies for the lead times from +7 to +18 h (with output from the 12:00 UTC model initialization, respectively). Similarly to the observation-based models, the performance of HRES-based models decreases with longer lead times, however much slower than with observation-based models. Persistence performs better than HRES-based boosting trees only up to a lead time of +2 h. Between the lead times +3 and +7 h the performance of the HRES-based models caught up to the observation-based ones. Observation-based boosting trees therefore perform on average better until a lead time of +5 h.
The best performing boosting trees are the ones with the combined predictor setup. With nowcasts of up to a +2 h lead time, they perform almost identically to observation-based models. During the lead times from +5 to +7 h they outperform both other models. Primarily, they perform similarly to observation-based models and converge slowly to the performance of the HRES-based boosting trees.
To analyze the performance of the boosting trees relative to other statistical models, we compare them to OLR. Figure 1b shows the RPSS comparison between the boosting trees and the OLR for the particular predictor setups. Boosting trees outperform OLR at most lead times. The biggest difference in forecast performance between both models is for the combined predictor setup (observations and NWP), where the boosting trees perform on average about 10 % better than OLR at short lead times. With increasing lead times, the difference in forecast performance between both models decreases, since the predictive power of the input variables becomes weaker.
When using only observations or HRES model output as predictors, the boosting trees perform again better than OLR, however with a lower improvement compared to the combined predictor setup. The reason for the higher improvement in boosting trees with the combined predictor setup is the integrated variable selection algorithm of the decision trees in the boosting model. Hence, only predictors that improve the predictive performance of the model are selected for forecast generation. In contrast, all available predictors are used for the forecast generation with standard OLR, as augmenting this model with automatic variable selection techniques would either be computationally intensive (e.g., stepwise or subset selection) or necessitate switching to another estimation technique (e.g., lasso instead of standard maximum likelihood).
The high variability in the RPSS analysis indicates the high complexity of predicting lvp states. Generally, fog can arise and dissipate with small atmospheric changes, leading to big challenges in forecasting this parameter numerically (Gultepe et al., 2007). At Vienna International Airport, severe lvp events (lvp1, lvp2, and lvp3) occur for only 10 % of the time. This low occurrence probability and fast transitions between particular states challenge the forecasts additionally. Moreover, with cross validation, the number of severe lvp events in the particular training samples can differ strongly, leading to varying performances for the particular cross-validated models and in an increased model variability. The overall decrease in forecast performance with time seen in the increase in RPS in Fig. 1a is halted at the +4 h forecast step (10:00 UTC), when the climatological frequency of LVP events decreases strongly (see Kneringer et al., 2019). The complexity of the forecasting problem can also be seen at the end of the climatological LVP minimum at +9 and +11 h (15:00 and 17:00 UTC), when the improvement in the tree-based methods over OLR in Fig. 1b suddenly drops.
Predictions of the models with the combined predictor setup are best overall; however, they also have the highest variability. Their forecasts are affected by many predictors and lead to stronger varying forecasts for the particular models due to the varying weights of the predictors. To provide information on the most important predictors with different lead times, variable importance analysis is applied.
4.1.2 Impact of predictors
The predictors with the highest impact on the forecast are analyzed with permutation importance applied to the boosting trees with the combined predictor setup (Sect. 3.3). Figure 2 shows the predictors with the highest impact on forecasts for the lead times +1, +6, and +12 h.
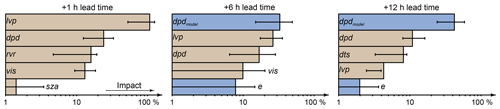
Figure 2Predictors of Table 2 with the highest impact on boosting trees with the combined predictor setup for lead times of +1, +6, and +12 h. The tan color indicates observation-based predictors, and the blue color indicates HRES-based ones. The x axis is logarithmic and shows the mean percentage decrease in forecast performance when the true values of the particular predictor are replaced with random information. The error bars show the 25th to 75th percentiles of the performance decrease for the particular predictors.
Forecasts with a lead time of +1 h mainly rely on observations. The most important input is the lvp state observation at forecast initialization, which would worsen the model performance by 107 % on average if its value is random. Other important observations are dpd, rvr, and vis, while the solar zenith angle (sza) and the remaining predictors contribute only little information. The importance of these inputs, however, varies by the same magnitude as their average, indicating the high complexity of predicting lvp states. Models with slightly different training samples can generate strong varying weights for their input variables. Nevertheless, the results of permutation importance for a +1 h lead time show the strong dependence of the short-term forecasts on observations and confirm the results in Fig. 1a, where the performance of the “best” models (combined predictor setup) is nearly identically to observation-based models.
The impact of observations decreases strongly for nowcasts with lead times from +3 to +7 h. Dew point depression from the NWP model (dpdmodel) and from the observations as well as lvp observations have the highest impact at +6 h forecasts. Further variables, albeit with smaller impact and higher variability, are observations of visibility and evaporation (e) from the NWP model output. In some of the cross-validated models, these two inputs have no impact on the predictions, while in others their impact is large.
As the forecasting horizon increases from +8 to +18 h, the influence of dew point depression from the NWP model increases, whereas other predictors only have small impact. Random lvp states at forecast initialization, for example, would decrease the performance by less than 5 % for predictions with a +12 h lead time. The performance of the models with the combined predictor setup is similar to the performance of the HRES-based models. The strong influence of NWP model-based dew point depression on the forecast performance confirms this finding.
4.2 Medium-range forecasts and predictability limit
The performance of models with the combined predictor setup converges to HRES-based models at lead times longer than +7 h (Fig. 1a). Therefore, we only use predictors based on the NWP model for the generation of medium-range forecasts and the investigation of the predictability limit. The predictors used include deterministic information from the HRES model and the means and standard deviations from the ENS.
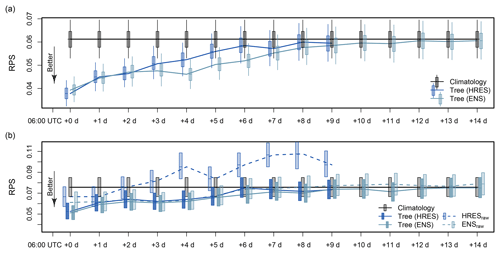
Figure 3Medium-range forecast performance of boosting trees based on HRES and ENS information, and the reference models with their uncertainty (boxes show the 25th to 75th percentile range, and whiskers show the 5th to 95th percentiles). (a) Median forecast performance of the statistical models and climatology for the complete 6 years of data (cold season only). (b) Median forecast performance of the statistical models and the references climatology and raw NWP model output (HRESraw, ENSraw) for December 2016–March 2017 and October–November 2017 only. The lvp state from the raw ensemble is computed from the distribution of the lvp states from each member. Computing the lvp state from only mean visibility and mean ceiling always results in lvp0. All lvp cases from the raw model output are due to low ceiling.
4.2.1 Model performance
Figure 3 shows the performance of boosting trees based on outputs of the HRES model and ENS for medium-range forecasts with lead times from +0 to +14 d. The predictions consist of output of the 00:00 UTC NWP model run, and the forecast validation time is again 06:00 UTC. Lead times of +0, +1, +2 d, etc., correspond to +6, +30, +54 h, etc. The maximum output length of the HRES model is +240 h. HRES-based model forecasts can be generated therefore only up to a +9 d lead time. The ENS, on the other hand, allows forecasts up to a +14 d lead time. We compare the performance of the statistical models only to the references climatology and raw NWP model output, since boosting trees again perform better than OLR (see Appendix B).
The performance of the boosting trees and climatology is shown in Fig. 3a with their uncertainties. HRES-based statistical models perform slightly better than ENS-based ones for lead times of +0 d. From +1 d to +2 d lead time, both models perform similarly, and after a lead time of +2 d, the ENS-based models perform better. The biggest difference in forecast performance occurs for the lead times from +4 to +6 d, where ENS-based models clearly outperform HRES-based ones, which converge much faster to climatology. The predictability limit, where the forecasts of climatology and the statistical models perform similarly in their median RPS, is at a lead time of approximately +12 d.
In order to obtain more information of the benefit of the statistical models, we compare them to the raw output of the NWP models. The raw lvp state is computed from the visibility and ceiling of the NWP model output. Since ceiling has been only available from November 2016 on, an out-of-sample comparison between the forecasts of the statistical models and the raw NWP model output is computed between December 2016 and November 2017 (cold season only). We therefore train the boosting trees with cold season data from December 2011 to November 2016 and compare their performance with the raw NWP model output for the remaining period.
Figure 3b shows the median out-of-sample performance of the statistical models, raw NWP model output, and climatology with their uncertainty for cold season data between December 2016 to November 2017. This period had a much higher occurrence of severe lvp than climatologically expected (see Fig. 3a).
HRES-based raw output performs better than climatology only up to +1 d. Direct output from the ENS, however, has a benefit over climatology up to a +5 d lead time. The statistical models with input from the ensemble model have a benefit over the raw ENS output up to the maximum available lead time of +14 d and remain better than climatology up to +11 d. Note that all lvp cases detected in the individual ensemble members have their origin in low-ceiling cases. The ECMWF visibility does not fall below the lvp threshold range during the test period. Moreover, raw lvp state forecasts from the ensemble average visibility and ceiling always result in lvp0. The reason is the exceeding of the lvp thresholds in the variable means for the entire data set.
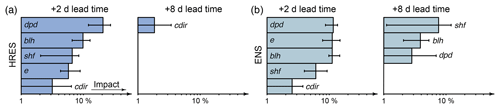
Figure 4Predictors of Table 2b with the highest impact for medium-range forecasts with +2 and +8 d lead times. The x axis is logarithmic and shows the percentage decreasing in performance when replacing the true observation of a particular predictor with random information. The error bars show the 25th to 75th percentiles of the decrease in forecast performance for the particular predictors. (a) HRES-based models. (b) ENS-based models.
4.2.2 Highest-impact inputs
The most important predictors for statistically based medium-range lvp forecasts are again analyzed with permutation importance. Figure 4 shows the predictors with the highest impact for the models based on the HRES model and ENS for the lead times of +2 and +8 d. In case of the ENS-based models, almost only predictors with mean information have an impact on the forecast, while the standard deviation contributes only little information.
Dew point depression (dpd) has highest impact for both models with a +2 d lead time. The performance of HRES-based models decreases by 21 % on average when observations are replaced by random values. Additional impact on the forecast originates from the predictors boundary layer height (blh), sensible heat flux (shf), evaporation (e), and clear sky direct solar radiation (cdir).
When the skill of the model forecasts over climatology decreases, the number of predictors with an impact on the forecast also decreases. In HRES-based models, only one predictor has an influence on predictions with +8 d lead times. Moreover, the impact of this predictor decreases strongly compared to the impacts of the predictors with the +2 d forecast. The convergence of the statistical models to climatology for longer lead times indicates low predictability of the predictors used from the NWP models, and therefore no stable association between the NWP output and the upcoming lvp state is found by the models. In ENS-based models, which perform better at long lead times, more predictors have an influence on the forecasts, and the impact of these predictors is generally bigger.
Predictions of lvp (low-visibility procedure) states have been developed for flight planning with different horizons using boosting trees. The lvp state, which is the relevant variable for flight regularization due to low visibility at airports, is categorical and consists of multiple thresholds of horizontal and vertical visibility. Former studies predict the horizontal and vertical visibility separately, which then can be combined by the air traffic management (e.g. Vislocky and Fritsch, 1997; Marzban et al., 2007; Ghirardelli and Glahn, 2010, etc.). This approach, however, makes accurate probabilistic forecasts of the lvp state impossible because of the interdependence of both visibility variables. Direct forecasts of the lvp states, on the other hand, allow probabilistic predictions of the information relevant for aviation. The lvp state predictions generated in this study are produced with boosting trees and are better (using the ranked probability score as verification metric) than forecasts from persistence, climatology, and ordered logistic regression models. The large variation of the benefit of the boosting trees over ordered logistic regression indicates the high complexity and the considerable challenge of generating lvp predictions due to fast transitions between particular lvp states. The forecasts are generated for timescales from +1 to +14 d, which are important for short-term regulation, flight plan reorganization, and long-term flight planning.
Short-term regulations are defined with predictions up to the next 2 h, which are most important for the flight controllers. These forecasts are the most accurate ones and are mainly driven by latest observations of the lvp state, dew point depression, and visibility.
For reorganizations of flight plans, the air traffic management can use the predictions with lead times from +3 to +18 h. Within this range, the impact of observations decreases and NWP model output becomes more important. Highly resolved deterministic NWP output leads to slightly better performance than ensemble information. For forecasts with lead times of +6 h, the NWP model output dew point depression and the observation of the lvp state have an equal impact. Hence, observations and NWP output have to be included in the statistical models to generate the most accurate predictions. The most important predictors are observations of the lvp state, horizontal visibility, dew point depression, air temperature difference between 2 m and the surface, and the NWP model outputs of dew point depression and evaporation.
Long-term flight planning requires medium-range forecasts with lead times longer than +1 d. During this time range, the statistical models with postprocessed ensemble information perform most accurately. The NWP outputs with the highest benefit for the predictions are dew point depression, evaporation, sensible heat flux, and boundary layer height. The predictability limit of lvp is approximately +12 d, where the benefit of the statistical forecasts over climatology vanishes.
The ECMWF NWP models also provide information on visibility and ceiling. Both variables can be used to predict lvp directly. However, these variables are not included in the statistical models because their data archive is too short. Comparisons between direct lvp state forecasts from the NWP models and the boosting trees were made for one cold season and just showed a small difference in the performance between a +1 and +5 d lead time. Therefore, the statistical models always perform somewhat better. The lvp state climatology of the comparison period, however, differs strongly from the climatology of the model training period, which suggests a comparison period that is too short for valuable statements. Nevertheless, for future investigations of the lvp state, NWP model output of ceiling and visibility should be included in the statistical models to improve the forecast performance. For both variables, however, information of each particular member should be taken into account instead of mean ensemble information, since the mean visibility and/or ceiling always leads to lvp-free conditions.
In summary, we saw that probabilistic lvp forecasts based on boosting trees have a benefit over all reference models until a lead time of approximately +12 d. These predictions can be used to improve flight planning at all required forecast horizons.
The complete statistical modeling is based on the software environment R (R Development Core Team, 2019). To estimate the boosting trees, the R package mboost (Hothorn et al., 2017) is used. The OLR models are estimated with the R package ordinal (Christensen, 2017), while the ranked probability score is computed with the R package verification (NCAR, 2015). The numerical weather prediction data are downloaded from the ECMWF. For observation data, a request to the Austro Control GmbH is required (info@austrocontrol.at).
For lvp state forecasts at Vienna International Airport, the log likelihood ℓ of the proportional odds model is defined as
The derivative of the log likelihood at Vienna International Airport is
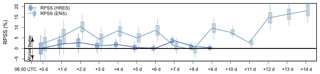
Figure B1RPSS comparison between boosting trees and ordered logistic regression for lead times from +0 to +14 d. For the boosting trees based on HRES NWP model output, the OLR based on HRES output is used as reference (boosting trees based on ENS output have OLR based on ENS output as reference). Higher RPSS shows better performance of the boosting trees over OLR. For forecasts with lead times longer than +11 d, the OLR is outperformed by climatology, whereas boosting trees still perform somewhat better than climatology. Thus, the boosting trees have high benefit over OLR at lead times longer than +11 d. The lines show the median RPSS, the boxes the 25th to 75th percentiles, and the whiskers the 5th to 95th percentiles.
The concept of this study was developed by all authors together. SJD conducted the majority of this paper, including statistical modeling, model evaluation, and paper writing. PK supported the statistical modeling and evaluation. GJM contributed meteorological expertise, while AZ contributed expert knowledge to statistical modeling. All the authors collaborated in discussing the results and commenting on the manuscript.
The authors declare that they have no conflict of interest.
This study has been supported by the Austrian Research Promotion agency FFG 843457 and the PhD scholarship of the University of Innsbruck. We want to thank Markus Kerschbaum, Andreas Lanzinger, Martin Steinheimer, and the meteorologists at Vienna International Airport for helpful discussions as well as Caren Marzban and Julie Bessac for their very constructive suggestions. Moreover, we thank the Austro Control GmbH for providing access to the observation data and the Zentralanstalt für Meteorologie und Geodynamik for providing the ECMWF data.
This paper was edited by Francis Zwiers and reviewed by Julie Bessac and Caren Marzban.
Agresti, A.: Categorical Data Analysis, John Wiley & Sons, Inc., 2003. a
Bocchieri, J. R. and Glahn, H. R.: Use of Model Output Statistics for Predicting Ceiling Height, Mon. Weather Rev., 100, 869–879, https://doi.org/10.1175/1520-0493(1972)100<0869:UOMOSF>2.3.CO;2, 1972. a
Breiman, L.: Random Forests, Mach. Learn., 45, 5–32, https://doi.org/10.1023/A:1010933404324, 2001. a
Bühlmann, P. and Hothorn, T.: Boosting Algorithms: Regularization, Prediction and Model Fitting, Stat. Sci., 22, 477–505, https://doi.org/10.1214/07-STS242, 2007. a, b, c
Christensen, R. H. B.: ordinal – Regression Models for Ordinal Data, available at: http://www.cran.r-project.org/package=ordinal/ (last access: 7 Juni 2017), R package version 2015.6-28, 2017. a
Dietz, S.J., Kneringer, P., Mayr, G. J., and Zeileis, A.: Forecasting Low-Visibilty Procedure States with Tree-Based Statistical Methods, Pure Appl. Geophys., 176, 2631–2644, https://doi.org/10.1007/s00024-018-1914-x, 2019. a, b, c, d, e
Dutta, D. and Chaudhuri, S.: Nowcasting Visibility During Wintertime Fog over the Airport of a Metropolis of India: Decision Tree Algorithm and Artificial Neural Network Approach, Nat. Hazards, 75, 1349–1368, https://doi.org/10.1007/s11069-014-1388-9, 2015. a
Epstein, E. S.: A Scoring System for Probability Forecasts of Ranked Categories, J. Appl. Meteorol., 8, 985–987, https://doi.org/10.1175/1520-0450(1969)008<0985:ASSFPF>2.0.CO;2, 1969. a
Federal Aviation Administration: Performance Specification PC Based Runway Visual Range (RVR) System, Tech. Rep. FAA-E-2772B, Department of Transportation, available at: https://www.faa.gov/about/office_org/headquarters_offices/ato/service_units/techops/navservices/lsg/rvr/media/FAA-E-2772B.pdf (last access: 30 June 2018), 2006. a
Ghirardelli, J. E. and Glahn, B.: The Meteorological Development Laboratorys Aviation Weather Prediction System, Weather Forecast., 25, 1027–1051, https://doi.org/10.1175/2010WAF2222312.1, 2010. a, b, c
Gultepe, I., Tardif, R., Michaelides, S. C., Cermak, J., Bott, A., Bendix, J., Müller, M. D., Pagowski, M., Hansen, B., Ellrod, G., Jacobs, W., Toth, G., and Cober, S. G.: Fog Research: A Review of Past Achievements and Future Perspectives, Pure Appl. Geophys., 164, 1121–1159, https://doi.org/10.1007/s00024-007-0211-x, 2007. a, b
Hamill, T. M., Hagedorn, R., and Whitaker, J. S.: Probabilistic Forecast Calibration Using ECMWF and GFS Ensemble Reforecasts. Part II: Precipitation, Mon. Weather Rev., 136, 2620–2632, https://doi.org/10.1175/2007MWR2411.1, 2008. a
Herman, G. R. and Schumacher, R. S.: Using Reforecasts to Improve Forecasting of Fog and Visibility for Aviation, Weather Forecast., 31, 467–482, https://doi.org/10.1175/WAF-D-15-0108.1, 2016. a, b, c
Hothorn, T., Hornik, K., and Zeileis, A.: Unbiased Recursive Partitioning: A Conditional Inference Framework, J. Comput. Graph. Stat., 15, 651–674, https://doi.org/10.1198/106186006X133933, 2006. a
Hothorn, T., Buehlmann, P., Kneib, T., Schmid, M., and Hofner, B.: mboost: Model-Based Boosting, available at: https://CRAN.R-project.org/package=mboost (last access: 7 June 2017), R package version 2.8-0, 2017. a
International Civil Aviation Organization: Manual of Runway Visual Range Observing and Reporting Practices, Tech. Rep. Doc 9328 AN/908, available at: http://dgca.gov.in/intradgca/intra/icaodocs/Doc (last access: 30 June 2018), 2005. a
Janjic, T., Bormann, N., Bocquet, M., Carton, J. A., Cohn, S. E., Dance, S. L., Losa, S. N., Nichols, N. K., Potthast, R., Waller, J. A., and Weston, P.: On the Representation Error in Data Assimilation, Q. J. Roy. Meteor. Soc., 144, 1257–1278, https://doi.org/10.1002/qj.3130, 2018. a
Kneringer, P., Dietz, S., Mayr, G. J., and Zeileis, A.: Probabilistic Nowcasting of Low-Visibility Procedure States at Vienna International Airport During Cold Season, Pure Appl. Geophys., 176, 2165–2177 https://doi.org/10.1007/s00024-018-1863-4, 2019. a, b, c, d, e, f
Leyton, S. M. and Fritsch, M.: Short-Term Probabilistic Forecasts of Ceiling and Visibility Utilizing High-Density Surface Weather Observations, Weather Forecast., 18, 891–902, https://doi.org/10.1175/1520-0434(2003)018<0891:SPFOCA>2.0.CO;2, 2003. a
Leyton, S. M. and Fritsch, J. M.: The Impact of High-Frequency Surface Weather Observations on Short-Term Probabilistic Forecasts of Ceiling and Visibility, J. Appl. Meteorol., 43, 145–156, https://doi.org/10.1175/1520-0450(2004)043<0145:TIOHSW>2.0.CO;2, 2004. a
Marzban, C., Leyton, S., and Colman, B.: Ceiling and Visibility Forecasts via Neural Networks, Weather Forecast., 22, 466–479, https://doi.org/10.1175/WAF994.1, 2007. a, b
Murphy, A. H.: A Note on the Ranked Probability Score, J. Appl. Meteorol., 10, 155–156, https://doi.org/10.1175/1520-0450(1971)010<0155:ANOTRP>2.0.CO;2, 1971. a
NCAR: Research Applications Laboratory, verification: Weather Forecast Verification Utilities, available at: https://CRAN.R-project.org/package=verification (last access: 7 June 2017), R package version 1.42, 2015. a
R Development Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, available at: http://www.R-project.org (last access: 30 March 2019), 2019. a
Roquelaure, S., Tardif, R., Remy, S., and Bergot, T.: Skill of a Ceiling and Visibility Local Ensemble Prediction System (LEPS) According to Fog-Type Prediction at Paris-Charles de Gaulle Airport, Weather Forecast., 24, 1511–1523, https://doi.org/10.1175/2009WAF2222213.1, 2009. a
Schmid, M., Hothorn, T., Maloney, K. O., Weller, D. E., and Potapov, S.: Geoadditive Regression Modeling of Stream Biological Condition, Environ. Ecol. Stat., 18, 709–733, https://doi.org/10.1007/s10651-010-0158-4, 2011. a, b, c
Strobl, C., Malley, J., and Tutz, G.: An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of Classification and Regression Trees, Bagging, and Random Forests, Psychol. Meth., 14, 323–348, https://doi.org/10.1037/a0016973, 2009. a
Vislocky, R. L. and Fritsch, M. J.: An Automated, Observations-Based System for Short-Term Prediction of Ceiling and Visibility, Weather Forecast., 12, 31–43, https://doi.org/10.1175/1520-0434(1997)012<0031:AAOBSF>2.0.CO;2, 1997. a, b, c
Wilks, D.: Statistical Methods in the Atmospheric Sciences, Academic Press, 2011. a
Wilks, D. S. and Hamill, T. M.: Comparison of Ensemble-MOS Methods Using GFS Reforecasts, Mon. Weather Rev., 135, 2379–2390, https://doi.org/10.1175/MWR3402.1, 2007. a
- Abstract
- Introduction
- Data
- Statistical framework
- Results
- Discussion and conclusion
- Code and data availability
- Appendix A: Log likelihood of the proportional odds model
- Appendix B: Comparison between boosting trees and ordered logistic regression for long-term flight planning ranges
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Data
- Statistical framework
- Results
- Discussion and conclusion
- Code and data availability
- Appendix A: Log likelihood of the proportional odds model
- Appendix B: Comparison between boosting trees and ordered logistic regression for long-term flight planning ranges
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References





