Evaluating skills and issues of quantile-based bias adjustment for climate change scenarios

Daily meteorological data such as temperature or precipitation from climate models are needed for many climate impact studies, e.g., in hydrology or agriculture, but direct model output can contain large systematic errors. A large variety of methods exist to adjust the bias of climate model outputs. Here we review existing statistical bias-adjustment methods and their shortcomings, and compare quantile mapping (QM), scaled distribution mapping (SDM), quantile delta mapping (QDM) and an empiric version of PresRAT (PresRATe). We then test these methods using real and artificially created daily temperature and precipitation data for Austria. We compare the performance in terms of the following demands: (1) the model data should match the climatological means of the observational data in the historical period; (2) the long-term climatological trends of means (climate change signal), either defined as difference or as ratio, should not be altered during bias adjustment; and (3) even models with too few wet days (precipitation above 0.1 mm) should be corrected accurately, so that the wet day frequency is conserved. QDM and PresRATe combined fulfill all three demands. For (2) for precipitation, PresRATe already includes an additional correction that assures that the climate change signal is conserved.

1 Introduction

Daily data from climate models are used for various applications, e.g., in hydrology, silviculture and for general climate risk studies (e.g., Horton et al., 2017; Seidl et al., 2019). However, simulated outputs from global climate models (GCMs) and regional climate models (RCMs) can exhibit large systematic biases relative to observational data sets (Mearns et al., 2013; Sillmann et al., 2013). Such systematic errors can be statistically adjusted with gridded observations. Those adjusted data sets are widely used (e.g., Bao and Wen, 2017; Thrasher et al., 2012; Chimani et al., 2016) but are controversial due to various errors introduced by statistical adjustment. Later in the introduction we postulate three demands we have for bias correction which were the result of reviewing several methods for statistical bias adjustment.

Simple methods that only correct the mean and/or the variance of the model data have been introduced (Maraun, 2016; Lafon et al., 2013; Widmann et al., 2003) and are still in use due to their simplicity (Navarro-Racines et al., 2020). Models may have different biases for extremes than for average values (Di Luca et al., 2020a, b). To improve the distribution of meteorological variables, more sophisticated approaches have been introduced. They adjust every quantile of the cumulative distribution functions (CDFs) according to the differences between daily modeled and observational data during a reference period. There are many different variations and names for this method in the literature: variable correction method (Déqué, 2007), distribution-based scaling (Yang et al., 2010; Seaby et al., 2013), distribution mapping (Teutschbein and Seibert, 2012), statistical bias-correction (Piani et al., 2010), statistical transformation (Gudmundsson et al., 2012), quantile–quantile mapping (Hatchett et al., 2016; Potter et al., 2020; Charles et al., 2020) or quantile mapping (QM) (Lafon et al., 2013; Themeßl et al., 2011; Maraun, 2016).

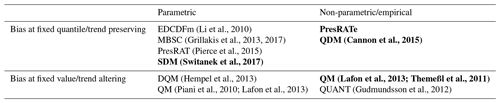
The distribution of meteorological variables can be described with empirical CDFs which is a non-parametric approach (e.g., Cannon et al., 2015). Many QM methods use a parametric approach instead (e.g., Hempel et al., 2013; Piani et al., 2010; Switanek et al., 2017), where statistical functions such as gamma or normal distributions are fitted to the CDFs. Whether to use a non-parametric or a parametric approach is still in scientific discussion (Teng et al., 2015), but the non-parametric approach is more common. Lafon et al. (2013) compared non-parametric (empirical) and parametric QM and found that the empirical approach was the most accurate. Cannon et al. (2015) and Gudmundsson et al. (2012) also prefer the empirical QM. Themeßl et al. (2012) point out that parametric QM can introduce new biases, because the distribution of a meteorological variable is not fully known and also depends on the region and season. However, non-parametric QM depends more on the calibration period than parametric QM. Switanek et al. (2017) argue that the correction of extremes is more robust with a parametric approach, as the return level of the most extreme event is somewhat random. This can be improved by fitting function to the distributions. Examples for the classification of methods as parametric or non-parametric is shown in Table 1.

One key feature of traditional QM is that it may alter the raw climate change signal (CCS) found in the model (i.e., the change of the arithmetic mean of a meteorological variable over time) (Hagemann et al., 2011; Maurer and Pierce, 2014; Maraun, 2013, 2016). This may sometimes be a desired feature, as the CCS of the model itself could be biased (Boberg and Christensen, 2012; Gobiet et al., 2015). In some cases, it has been argued that CCS-changing bias-adjustment methods may even improve implausible trends (Maraun et al., 2017). Particularly, if the model has large errors in circulation patterns, CCS-preserving bias adjustment may amplify the bias (Maraun et al., 2021) and thus lead to implausible trends.

This means that the choice of a climate model with plausible weather patterns and a plausible CCS is crucial (Maraun et al., 2021). If the trend simulated by the model is trustworthy (see Sect. 12 in Maraun and Widmann, 2018 for further discussion on this topic), one might want to keep the trend unchanged after bias adjustment. As a workaround for trend preservation, Bürger et al. (2013) and Hempel et al. (2013) removed the trend before QM and added the trend back again after bias adjustment (detrended quantile mapping – DQM). A trend-preserving method termed as quantile delta mapping (QDM) was developed by Cannon et al. (2015). It was implemented as a parametric, slightly changed method by Switanek et al. (2017) who named their approach scaled distribution mapping (SDM). A very similar approach termed the equidistant CDF matching method (EDCDFm) was introduced by Li et al. (2010) which was later improved by Pierce et al. (2015). Cannon et al. (2015) prove in their appendix that EDCDFm and QDM are equivalent in the end however different they are in concept.

Bias adjustment methods that do not alter the CCS implicitly assume time invariance (Maraun and Widmann, 2018) for the bias, i.e., that the mean bias is time-independent and therefore the predicted trends are credible. Methods that do not alter the CCS include MBSC (Grillakis et al., 2013, 2017), QDM, PresRat, EDCDFm and SDM. In the end, all five of these methods assume that the biases at quantiles do not change over time (overview in Table 1). In contrast, QM implicitly assumes a constant bias at a certain value and determines the quantile for a given future value from the calibration distribution (hence the name quantile mapping). In other words, QM assumes stationarity of the bias for each quantile with quantiles derived from the calibration distribution regardless of whether a value is taken from the calibration or from the future periods. QDM and similar methods assume a stationary bias for each quantile but with the quantiles for a value from the future period derived from the future distribution.

Note that the definition of the time-invariance assumption, sometimes also called stationarity assumption (Switanek et al., 2017), is inconsistent in the literature. For example, Switanek et al. (2017) state that standard QM has the underlying assumption of time-invariant stationarity contradicting Maraun and Widmann (2018). We assume these inconsistencies come from different definitions. Stationarity can refer to a time-independent mean bias or to a time-independent bias found at certain absolute values of a meteorological variable. Since QM does alter the CCS, we conclude that QM implies that the mean bias changes over time.

EDCDFm and QDM are always capable of preserving the CCS in the median (and also at every quantile). If applied additively, this also holds true for the arithmetic mean. For precipitation, a multiplicative approach is more suitable. Pierce et al. (2015) call the multiplicative method PresRAT; it preserves the model-predicted CCS in median (and also at every quantile) but not the mean CCS. It may make sense to correct the mean CCS on a monthly, seasonal or annual basis after bias adjustment (Pierce et al., 2015).

Most of the bias-correcting methods correct a wet day bias of a climate model (i.e., the number of wet days above a specific precipitation threshold) only if the model has a positive wet day bias. However, in some rare cases, the model may have too few wet days. Often, a multiplicative bias adjustment is selected for precipitation (e.g., Switanek et al., 2017; Pierce et al., 2015; Cannon et al., 2015). To avoid division by zero during bias adjustment, dry days have to be treated separately. Only few studies have focused on correcting a negative wet day bias, with one of them being Themeßl et al. (2012). They use a simple linear interpolation to fill the gap of wet days in the precipitation CDF. This does not necessarily conserve precipitation sums, because the CDF of precipitation does not follow a linear curve. Some authors solved this problem by modifying the dry days prior to bias adjustment (Cannon et al., 2015; Cannon, 2018; Mehrotra et al., 2018; Vrac et al., 2016). The latter authors named the method singularity stochastic removal (SSR). This method is already part of QDM from Cannon et al. (2015) and in PresRAT from Pierce et al. (2015), although in their papers there is no explicit name for this wet day correction.

There is no single best bias-adjustment method that fits all needs. The advantages and disadvantages of the bias-adjustment methods mentioned here depend on the application. Maraun and Widmann (2018) and Doblas-Reyes et al. (2021) comprehensively review the whole topic, the motivation behind bias adjustment and the historic development. Generally speaking, distribution-based methods like QM usually outperform other simpler methods like mean bias adjustment, as shown by Lafon et al. (2013) or Themeßl et al. (2011). In Pierce et al. (2015), EDCDFm is preferred over QM because it does not alter the CCS. Casanueva et al. (2020) tested SDM, DQM, QDM, an empirical and a parametric QM, and others and concluded that trend-preserving methods like SDM and DQM are preferable. Large comparative studies (Maraun et al., 2019; Gutiérrez et al., 2019; Widmann et al., 2019) provide an overview of many bias-adjustment methods.

The goal of this paper is to find a suitable quantile-based bias-adjustment method that could be used for climate impact modeling studies that are sensitive to the changes in means to thresholds effects. In the course of this, we will also show the systematical differences of several methods. We choose to focus only on quantile-based methods, because they usually outperform simpler methods, as described above. We posit that three important demands should be met:

1. The bias-adjusted data should match the observational data in the historical period in terms of arithmetic mean.

2. The CCS should not be altered during bias adjustment. In other words the mean change between historical and simulated future period from the raw model should be preserved. This should also hold true for the ratio of the CCS, if the bias adjustment is applied multiplicatively.

3. Models with too few wet days should be corrected reasonably, which means that a way has to be found to add wet days.

In this paper we compare how well certain quantile-based bias-adjustment methods meet these three demands. SDM is selected because it has been used for larger projects in Austria (Chimani et al., 2016, 2019), it outperforms other methods (Casanueva et al., 2020) and it is a parametric method. Traditional empirical QM is widely used and is part of many comparison studies (Widmann et al., 2019; Maraun et al., 2019; Pierce et al., 2015; Casanueva et al., 2020; Smith et al., 2014). As a third method, we use either QDM (Cannon et al., 2015) or PresRAT (Pierce et al., 2015). The latter is only used for precipitation, and the slight difference between the two methods is described in Sect. 3.3. We apply them in an explicitly empirical (non-parametric) manner, as we experienced problems with fitting functions to the CDF of daily precipitation values (Vlček and Huth, 2009). This empirical aspect is an important feature of these two methods. In Pierce et al. (2015) it is not clearly stated if PresRAT is an empiric or a parametric approach. Table 1 shows a classification of quantile-based bias-adjustment methods. The methods in bold are used in this paper and are representatives of all methods that are within each of the groups.

(Li et al., 2010)(Grillakis et al., 2013, 2017)(Cannon et al., 2015)(Pierce et al., 2015)(Switanek et al., 2017)(Hempel et al., 2013)(Lafon et al., 2013; Themeßl et al., 2011)(Piani et al., 2010; Lafon et al., 2013)(Gudmundsson et al., 2012)

Table 1 Grouping of some quantile-based bias-adjustment methods in two categories. Note that this list is not complete. The methods in bold are used in this work.

2 Data and area of interest

This study focuses on Austria which is located in Central Europe and is representative of a mountainous area in the middle latitudes. The topography is shown in Fig. 1. A large part of the Eastern Alps are within the Austrian borders. The elevation ranges from 114 m in the east of Austria to 3798 m a.m.s.l. on the highest mountain. Because of the complexity of the topography, the spatial resolution of GCMs and also RCMs is not sufficient to resolve mountain ridges and valleys. The climatological properties can change within a few kilometers due to topographically induced effects (Stauffer et al., 2017).

Figure 1 Area of interest with Austrian state borders. © European Union, Copernicus Land Monitoring Service 2020, European Environment Agency (EEA).

Austria has a large number of high-quality weather observation stations that are operated by Zentralanstalt für Meteorologie und Geodynamik (ZAMG). Also, gridded observational data sets called SPARTACUS for minimum temperature, maximum temperature and precipitation are available on a daily basis at a high spatial resolution of 1 km (Hiebl and Frei, 2016, 2018). The time span reaches from the year 1961 to 2019. SPARTACUS mostly uses stations with long time series to provide robust trends for climate change.

For the observational data, SPARTACUS (Hiebl et al., 2020) in its unchanged form is used (hereafter named OBS). For model data, synthetic data are produced by smoothing SPARTACUS data with a running mean of 12 km. This is a typical spatial resolution of RCMs.

To generate artificial data with loo few wet days and too little precipitation, the data were further manipulated. This was done by multiplying the precipitation of each day with a uniformly distributed random number between 0 and 1. Furthermore, a trend to even drier conditions was introduced by successively canceling more and more wet days going from 1961 to 2019.

To show that the bias-adjusted model data do not always match the observations in the historical period, we analyzed data sets in Austria from the projects ÖKS15 (Chimani et al., 2016; Leuprecht, 2016) and STARC-Impact (Chimani et al., 2019). In both projects, the model data (Mendlik, 2018) were bias adjusted with SDM (Switanek et al., 2017). These data are freely available via the Climate Change Center Austria (CCCA) and consist of bias-adjusted temperature and precipitation data from several RCMs at a spatial resolution of 1 km. The data are used for many climate impact studies in Austria (e.g., Jandl et al., 2018; Unterberger et al., 2018).

We calculated climatological annual precipitation sums for all models in ÖKS15 and STARC-Impact in the reference period 1971–2000 and for the observation data set GPARD1 for the same time period (e.g., Chimani et al., 2016; Hofstätter et al., 2015). This period was used for bias adjustment in the two projects. The bias for each model in the period 1971–2000 is calculated as the difference between the mean of models and observation. Figure 2a shows the bias of the domain average annual precipitation for each model. The mean bias ranges from approx. −6 % for the driest model to +2 % for the wettest model. The comparison on a grid cell basis on the right side in (Fig. 2b) shows biases of more than 5 % for the wettest 0.1 percentile, and a bias of approx. −25 % for the driest grid cells. However, the median bias of all models is +0.5 %, which we consider as quite good.

Looking further into all the models used in ÖKS15 and STARC-Impact, we found that the largest errors occur in very dry models with a distinct negative wet day bias. Therefore, we focus on the bias adjustment of very dry climate models in this paper.

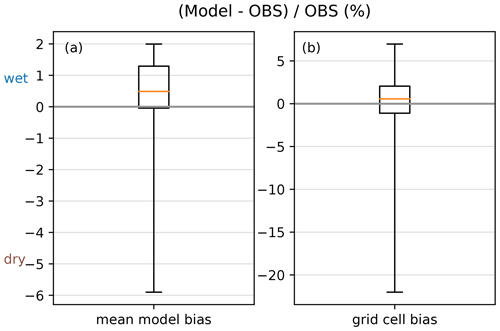
Figure 2 Box and whisker plot for the relative annual precipitation bias (%) of the ÖKS15 and STARC-Impact models (a total of 35 models) to the observational data set GPARD1 for the reference period 1971–2000. A positive bias indicates that the model is wetter than the observations. (a) Relative bias for the area mean for each climate models in Austria. (b) Relative bias on a grid cell basis. The upper (lower) whisker shows the 99.9 (0.1) percentile. The box ranges from the 25th to the 75th percentile, the horizontal orange line shows the median.

3 Methods

This study focuses on implementing QDM and PresRATe to bias-correct data from climate models and compares it with two existing methods, namely QM and SDM. All methods are quantile-based bias-adjustment methods that adjust the climate model data to match the CDF of the observation. The daily data of each grid cell of the model are adjusted separately with the observations on a monthly basis. For the calibration data, a time period of 30 years is typical, since the statistical distribution of data of a shorter time period can be very noisy and a longer time period usually has pronounced climatological trends.

3.1 Systematical differences of quantile-based methods

As discussed in the introduction, QM and QDM are systematically different when correcting future values. The model bias in QM is fixed on the quantiles from the calibration distribution, hence, it is fixed on absolute values. QDM and similar methods assume a stationary bias for each quantile but with the quantiles for a value from the future period derived from the future distribution.

We postulate that the bias of a climate model is correlated to the modeled weather pattern. In other words, we consider that the RCM is able to predict a ranked category of temperature or precipitation but not the value for this variable (Déqué, 2007). If we assume that the frequency of weather patterns does not change significantly over time, this means that certain quantiles of temperature are linked to certain weather situations. Because QM corrects absolute values, regardless of the underlying weather conditions, trends are modified. Thus, if one wants to preserve trends, one must at least implicitly account for weather conditions. Now, we argue that QDM and similar methods do this implicitly, assuming that weather situation frequencies change little and that biases are primarily weather-situation-dependent not absolute-value-dependent: a weather situation in the future would then have a higher temperature value accordingly but still the same quantile. This becomes more obvious when shown in two examples:

• A cold winter day in Austria is related to moderate northeasterly flows and usually high atmospheric pressure with low wind and clear sky conditions. Cold translates to a low quantile for temperature. In future, the error of the model in this weather situation is assumed to stay constant. This weather situation will still translate to a low quantile in the future distribution, however, the absolute temperature values are higher (respectively, the corresponding quantile calculated from the historical distribution is higher).

• Consider the daily maximum temperatures for a grid point during a summer month in Europe, where three quantiles of the observations in the reference period are 20, 25 and 30 ^∘C. The model simulates 20, 30 and 32 ^∘C for the same period, i.e., there is a warm bias especially in the middle quantile. QM would suggest 0, −5 and −2 ^∘C as correction values for the model values. For the future period, the model simulates 25, 35 and 36 ^∘C. QM would correct this to 22.5, 33 and 34 ^∘C. In this example, values in between are linearly interpolated, values above the range in the reference period (above 32 ^∘C) are found through constant extrapolation; that is, the correction value for the highest temperature also applies for even higher temperatures. QDM corrects at quantiles (not fixed values) which yields to 25, 30 and 34 ^∘C. In this simple example, QDM seems to plausibly correct the model's warm bias at middle quantiles, while QM does not.

This means that the two systematically different ways to apply a quantile correction influences the result. Traditional QM may alter the raw CCS found in the model, while other methods like QDM and PresRAT do not. Preserving the CCS is a choice of the researcher and not an a priori given. Our approach of correcting quantiles is also supported by Maraun and Widmann (2018) who state that biases depend not only on the actual values but more generally on the state of the climate system. The effect of QM on the CCS can be seen in Fig. 3. The resulting CDF of QM is much warmer than the CDF of QDM. Also, Fig. 3 points out schematically where the correction values are applied on the CDFs.

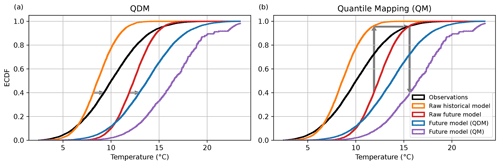
Figure 3 Schematic of bias adjustment for temperature data. CDFs are shown for following data: observational data (black), raw historical model (orange), raw future model (red), future model corrected with QDM (blue) and future model corrected with QM (purple). The arrows illustrate the bias-adjustment path for future model data. Panel (a) shows QDM, where the model bias in the calibration period (left arrow) is applied to the future model data (right arrow that has the same length as the left arrow). Panel (b) shows QM, where the correction value is found at the model bias in the historical period of the same absolute value.

3.2 PresRATe (precipitation) and QDM (all other variables)

QDM (Cannon et al., 2015) and PresRAT (Pierce et al., 2015) are trend-conserving methods. We apply these methods strictly non-parametrically, as we experienced problems with fitting functions to daily precipitation values (Vlček and Huth, 2009); hence, we add the letter “e” for empiric (PresRATe). QDM and PresRATe are almost equivalent. The difference between the two methods is that PresRATe adjusts the CCS after the bias adjustment of precipitation, so that either the mean monthly, seasonal or annual CCS of the raw model is conserved (Sect. 3.3).

The mathematical description of QDM and PresRATe is similar to EDCDFm in Eq. (2) in Li et al. (2010). The starting point is the second and third term on the right side of this equation which is the term that corrects the raw model data as follows:

$$\begin{array}{}\text{(1)}& x_{\mathrm{corr}}=x_{\mathrm{m}-\mathrm{f}}+\underset{\text{correction term}}{\underbrace{F_{\mathrm{o}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{m}-\mathrm{f}}\left(x_{\mathrm{m}-\mathrm{f}}\right)\right)-F_{\mathrm{m}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{m}-\mathrm{f}}\left(x_{\mathrm{m}-\mathrm{f}}\right)\right)}},\end{array}$$

where x_corr is the time series of the corrected variable, x_m−f is the original time series of the variable, and F is the CDF of either the observations (o) or model (m) for a historic (calibration) period (c) or future (projection) period (f). F is an empirical function in this and all following equations. The terms in brackets $\left(F_{\mathrm{m}-\mathrm{f}}\left(x_{\mathrm{m}-\mathrm{f}}\right)\right)$ are now replaced by F₁₀₀ that consists of 100 equidistant values from 0.5 % to 99.5 %, which are the 100 percentiles for which the CVs are defined through Eq. (4):

$$\begin{array}{}\text{(2)}& {\displaystyle }{F}_{\mathrm{100}}=\left(\begin{array}{c}\mathrm{0.995}\\ \mathrm{0.985}\\ \mathrm{\dots }\\ \mathrm{0.015}\\ \mathrm{0.005}\end{array}\right)\text{(3)}& {\displaystyle }\text{CV}=F_{\mathrm{o}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{100}}\right)-F_{\mathrm{m}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{100}}\right).\end{array}$$

The number of 100 points seems to be a reasonable compromise. A higher number would be less robust to extremes, as especially the CVs of extremes would depend even more on single extreme events. A lower number would provide less detail about the distributional shape of the model bias. In Eq. (3), the CVs are defined as the difference between two inverse CDFs which is used for variables such as temperature and dew point.

For variables that have a meteorologically meaningful zero value as a lower boundary, a multiplicative approach is more useful, e.g., for precipitation, wind speed or global radiation (see also Pierce et al., 2015). The CVs for those variables are found by

$$\begin{array}{}\text{(4)}& \text{CV}={\displaystyle \frac{F_{\mathrm{o}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{100}}\right)}{F_{\mathrm{m}-\mathrm{c}}^{-\mathrm{1}}\left(F_{\mathrm{100}}\right)}}.\end{array}$$

If the model wind speed and global radiation should ever reach exact zero in the denominator, Eq. (4) would not be defined. For this case, the corresponding CVs are manually set to 0. For precipitation, the procedure is described in Sect. 3.4. The CVs can be interpreted as the model bias for each quantile of the model data at a given grid cell.

Any desired time period for bias adjustment is selected (future or historical). It is possible to choose the calibration period itself. The time period to be chosen is usually a 30-year period, as for the calibration time period. For the final bias adjustment, the CVs are added (Eq. 4 for temperature and dew point) or multiplied (Eq. 5 for precipitation, global radiation and wind speed) to the selected (e.g., future) model data x_m-f. This results in the bias-corrected data x_corr. Mathematically, this can be described as

$$\begin{array}{}\text{(5)}& {\displaystyle }{x}_{\mathrm{corr}}=x_{\mathrm{m}\text{-}{\mathrm{f}}_{\mathrm{r}}}+{\text{CV}}_{\mathrm{i}}\text{(6)}& {\displaystyle }{x}_{\mathrm{corr}}=x_{\mathrm{m}\text{-}{\mathrm{f}}_{\mathrm{r}}}\cdot {\text{CV}}_{\mathrm{i}},\end{array}$$

where $x_{\mathrm{m}\text{-}{\mathrm{f}}_{\mathrm{r}}}$ is the ranked future model data and the CVs are interpolated to CV_i to match the length of $x_{\mathrm{m}\text{-}{\mathrm{f}}_{\mathrm{r}}}$. This ensures that every value of $x_{\mathrm{m}\text{-}{\mathrm{f}}_{\mathrm{r}}}$ is matched with the CV of the same quantile. For values within the range of F₁₀₀, the CVs are linearly interpolated. For extreme data at both ends of the distribution, the CVs have to be extrapolated. This is done via constant extrapolation, i.e., the first (last) CV is used for correcting data below (above) the outermost CDF value. All model data values below the 0.5 % percentile are corrected with the CV attached to the 0.5 % percentile, and model data values above the 99.5 % percentile are corrected with the CV attached to the 99.5 % percentile. As the result, x_corr is also ranked, the values have to be rearranged in the original order in the time series.

The graphical solution for bias adjustment for temperature data is shown in Fig. 3. The temperature data in this plot are artificially created following a normal distribution, where the historical period is 1981–2010 and the future period is 2071–2100. In this hypothetical case, the present-day model has a significant bias in mean and variance as follows:

• The observational data feature a mean of 10 ^∘C and a standard deviation of 3.1 ^∘C.

• The raw historical model (1981–2010) has a cold bias in the data with a mean of 8 ^∘C and a standard deviation of 1.8 ^∘C.

• The raw future model (2071–2100) is warmer with a mean of 12.4 ^∘C, but the standard deviation remains unchanged to the historical model with a standard deviation of 1.8 ^∘C.

For the raw historical model, these distributions result in too low temperatures at the upper end of the CDF and slightly too high temperature at the lower end. During the bias adjustment of QDM, this model bias of each quantile is added to the future model resulting in the bias-corrected model (purple line). In contrast, QM uses absolute model values from the historical period. As during climate change, higher temperatures occur more often, correction values from the upper part of the CDF are used more often. As higher temperatures tend to have larger biases in the raw historical model, the adjustment with QM results in a bias-adjusted model that is too warm.

3.3 Precipitation: conserving the CCS

QDM and PresRATe (Sect. 3.1) conserve the raw model's CCS on each quantile. For additive bias adjustment (used for temperature and dew point), this is also valid for means and sums. However, pure multiplicative bias adjustment does not conserve the relative CCS of means for precipitation. As the precipitation sum (monthly sum, annual sum) is usually more important than the precipitation at a specific quantile in the CDF, an additional algorithm is developed to reproduce the raw model's change in means. This is referred to as the conservation of the model CCS. Depending on the application of the corrected precipitation data, one can adjust the monthly, seasonal or the annual CCS. The following approach is equivalent to the ones in Pierce et al. (2015) and Charles et al. (2020).

For a future time period, the CCS for precipitation for the raw model for one grid point is

$$\begin{array}{}\text{(7)}& {\text{CCS}}_{\text{m}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{R_{\text{m-f}}}}{\stackrel{\mathrm{‾}}{R_{\text{m-c}}}}},\end{array}$$

where $\stackrel{\mathrm{‾}}{R_{\text{m-f}}}$ is the mean precipitation of the model in the future time period, and $\stackrel{\mathrm{‾}}{R_{\text{m-c}}}$ is the mean precipitation of the model in the historical (calibration) time period. The mean is either a monthly or annual climatological mean. The CCS for the bias-adjusted data after QDM is

$$\begin{array}{}\text{(8)}& {\text{CCS}}_{\text{corr}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{R_{\text{corr-f}}}}{\stackrel{\mathrm{‾}}{R_{\text{corr-c}}}}}.\end{array}$$

The error E of the CCS of the corrected model compared to the CCS of the raw model (in %) is defined as

$$\begin{array}{}\text{(9)}& E={\displaystyle \frac{{\text{CCS}}_{\text{corr}}}{{\text{CCS}}_{\text{m}}}}\cdot \mathrm{100}-\mathrm{100},\end{array}$$

where a value of 0 is a perfect bias-adjustment method. The precipitation (daily data) of the bias-adjusted model data R_corr-f,t for every day t is corrected with

$$\begin{array}{}\text{(10)}& R_{\text{corr CCS},t}=R_{\text{corr-f},t}\cdot {\displaystyle \frac{{\text{CCS}}_{\text{m}}}{{\text{CCS}}_{\text{corr}}}}\end{array}$$

to match the CCS of the raw model data (then called PresRATe) and makes the difference between QDM and PresRATe. Equations (7) and (8) can be applied for either monthly, seasonal or annual data, or for all, applied one after the other. However, every CCS cannot be exactly conserved at the same time, because the second CCS (e.g., the annual one) alters the data from the first CCS correction (e.g., monthly).

3.4 Precipitation: adding wet days QDM

All tested methods correct by default the number of wet days if the model has more wet days than the observational data by multiplying the lower parts of the model CDF by 0. However, a quantile-based bias adjustment cannot add wet days that are initially not in the model. This is already described in Cannon et al. (2015) for QDM and in Pierce et al. (2015) for PresRAT. Vrac et al. (2016) called this method singularity stochastic removal (SSR), and they provide a more detailed explanation. SSR corrects the number of wet days by replacing the zero precipitation days with a trace amount (below 0.05 mm) before calculating the correction values for the bias adjustment. This allows to use all days for bias adjustment, even the dry days, where otherwise zeros could cause problems during the bias adjustment when dividing by zero. After, bias-adjustment values below the trace amount are reset back to zero.

If we use QDM without SSR, we call this QDMd (d for dry).

3.5 Empirical quantile mapping (QM)

We compare the performance of QDM and PresRATe with other methods. One of them is the traditional QM in a non-parametric form, that is widely used (e.g., Piani et al., 2010; Themeßl et al., 2011; Teng et al., 2015; Gutiérrez et al., 2019; Maraun et al., 2019; Widmann et al., 2019). Quantile mapping in its original form is usually written as (Li et al., 2010; Themeßl et al., 2011)

$$\begin{array}{}\text{(11)}& x_{\mathrm{corr}}=F_{\text{o-c}}^{-\mathrm{1}}\left(F_{\text{m-c}}\left(x_{\text{m-f}}\right)\right),\end{array}$$

where F is the (in our case, empirical) CDF of either the observations (o) or model (m) for a historic (calibration period) climate (c) or future period (f). This QM cannot produce values that are outside the observed range. In the context of climate change, new extremes are considered via a simple extrapolation: For values that are above or below the most extreme values found in the observations, a constant correction of the last value is applied (Boé et al., 2007). For example, if the highest temperature found in the historical model is 34 ^∘C and the highest value in the observations is 36 ^∘C, a correction value of +2 ^∘C is applied to all future model values above 34 ^∘C. QM including extrapolation is written as

$$\begin{array}{}\text{(12)}& x_{\mathrm{corr}}=F_{\text{o-c}}^{-\mathrm{1}}\left(F_{\text{m-c}}\left(x_{\text{m-f}}\right)\right)+\underset{\text{Extrapolation term}}{\underbrace{x_{\text{m-f}}-F_{\text{m-c}}^{-\mathrm{1}}\left(F_{\text{m-c}}\left(x_{\text{m-f}}\right)\right)}}.\end{array}$$

This formula is used in this work and is part of the code in the pyCAT module for Python. The extrapolation term is zero when x_m-f lies within the range of historical model values. Comparing Eq. (12) with Eq. (1) shows that QM calculates the CDF from the model in the historical period (F_m-c), whereas QDM and PresRATe use data from the period where the correction is applied on (F_m-f).

3.6 Scaled distribution mapping (SDM)

SDM is a further development based on QDM and is explicitely parametric (Switanek et al., 2017). SDM is available via the pyCAT module for Python. SDM is a parametric method. For precipitation, gamma distribution can be selected. The parameters for the gamma distribution are found iteratively via the maximum likelihood function which can be computationally expensive. In our work, we observed the SDM script to be more than one order of magnitude slower than the other empiric bias-adjustment methods.

Tests showed that the fitting is sometimes defective and results in errors when the corrected model data are compared with the observations (see Fig. 2). Hence, the SDM script is not always able to reproduce the past climate by correcting the model according to the observations.

Therefore, we generated several versions of SDM. For this work, we improved the fitting of the gamma functions by adding initial guesses to the fitting function. According to the methods of moments (Thom, 1958; Wiens et al., 2003), the initial guess for the scale parameter θ for the gamma distribution is defined as

$$\begin{array}{}\text{(13)}& \mathit{\theta }={\displaystyle \frac{\text{Var}\left(X\right)}{\overline{X}}},\end{array}$$

where X is the data to be fitted, and $\overline{X}$ is the mean of the data. Optionally also the shape parameter k can be used for the initial guess as

$$\begin{array}{}\text{(14)}& k={\displaystyle \frac{{\overline{X}}^{\mathrm{2}}}{\text{Var}\left(X\right)}}.\end{array}$$

We used four different versions of SDM which are as follows:

• SDM(raw). This is the version of SDM as presented in Switanek et al. (2017). SDM(raw) lacks the correction of wet days, if the model has too few wet days.

• SDM(0). In addition to SDM(raw), corrected wet days are interpolated to the expected number of wet days which corrects a wet day bias. This algorithm was provided by the authors of Switanek et al. (2017).

• SDM(1). In addition to SDM(0), the shape parameter k is used as an initial guess for the gamma distribution of precipitation.

• SDM(2). In addition to SDM(0), both shape parameter k and scale parameter θ are used in the initial guess.

4 Results

QDM, PresRATe, QM and SDM are evaluated in terms of three demands expressed at the end of Sect. 1.

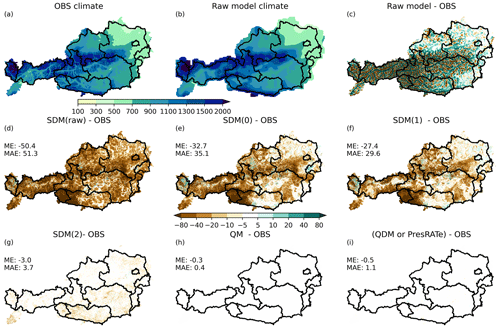
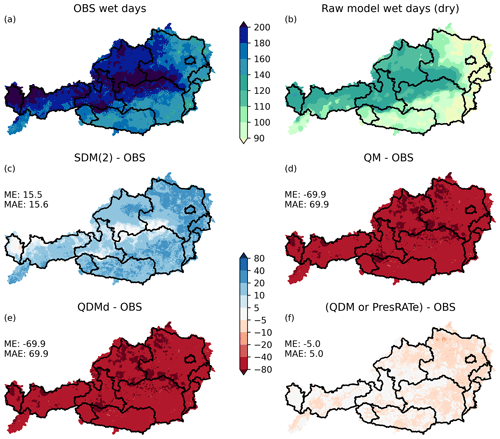
Figure 4 Bias adjustment of precipitation data. The model is produced by smoothing OBS. (a) Observational annual precipitation. (b) Raw model annual precipitation. (c) Difference of annual precipitation between model and observation. (d–i) Difference in annual precipitation (model minus observational data) in millimeters for (d) SDM(raw), (e) SDM(0), (f) SDM(1), (g) SDM(2), (h) QM and (i) QDM/PresRATe. ME – mean error. MAE – mean absolute error.

4.1 Demand (1): conservation of historical climate

The four versions of SDM are compared with non-parametric QM and QDM/PresRATe, respectively. We already showed that biases can be introduced by the bias-adjustment methods themselves with the example of ÖKS15 and STARC-Impact data (Fig. 2). To reproduce some of the biases, we used the smoothed observational data as produced in Sect. 2. Depending on the method of bias adjustment, even after correction, the bias can be significant (Fig. 4). Figure 4a is the observed average annual precipitation (OBS), where the impact of small-scale spatial patterns like valleys, mountains and windward and leeward side can be seen. Figure 4b is the artificial smoothed model but otherwise very similar to OBS. The only difference is the spatial resolution between OBS and the model. Figure 4c shows the difference between the observations and the model, which shows the patterns of the much finer resolution of the observations, like drier valleys and wetter mountains. Figure 4d–i shows the difference of the mean annual precipitation of the bias-adjusted model data minus the mean annual precipitation of the OBS.

Figure 4d uses SDM(raw) which produces the largest errors with a mean absolute error of 51.3 mm in annual precipitation. The difference in annual precipitation exceeds 100 mm in parts of East Tyrol and Carinthia (southwestern parts of Austria). The errors produced by SDM(0) and SDM(1) (Fig. 4e and f) are considerably smaller. The smallest errors are produced when using SDM(2), where the error is 10 mm or less in most parts of Austria with a mean absolute error of 3.7 mm yr⁻¹.

For comparison, the model data were corrected with other methods such as QM and QDM/PresRATe where the error is close to zero. This is because these methods calculate empirical CDFs of both model and OBS which produces very accurate results in the reference period.

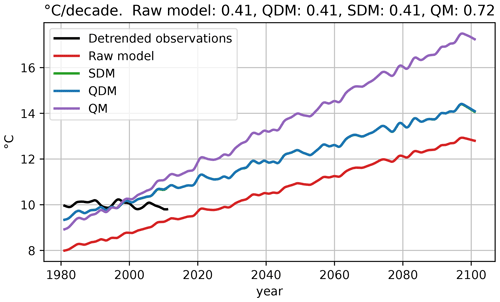
Figure 5 Running means of temperature data of detrended observations, the raw model and three different bias-correcting methods (QM, SDM and QDM). SDM and QDM are almost identical. On top: average linear trends in ^∘C per decade (1981–2100) for each bias-adjustment method. The data are identical to the data used in Fig. 3.

4.2 Demand (2): climate change signal (CCS)

Demand (2) for the bias adjustment is that the CCS of the raw climate model should not be altered. As stated by Maraun (2016), methods like standard QM modify the CCS of temperature where the CCS is defined as an absolute value. Therefore, we calculated the CCS for all three methods for temperature. As temperature data, we used the artificial data as generated in Sect. 3.2. The corresponding CDFs are shown in Fig. 3. In Fig. 5 we show the smoothed mean annual temperature for the detrended observations, the raw climate model and for the bias-corrected model data. The temperature of the raw model shows an increase of 0.41 ^∘C each decade. The bias-adjustment methods SDM and QDM reproduce the exact same trend and are thus able to exactly conserve the CCS. In contrast, QM inflates the climate change signal with a linear trend of 0.72 ^∘C per decade. We also tested all three methods with non-linear trends, where QM tends to inflate or deflate the CCS (not shown), while SDM and QDM keep the CCS unchanged.

For precipitation, the CCS is defined as a relative value as shown in Eqs. (7) and (8). The relative CCS is greater than 1 in case of more precipitation in the future. In Sect. 2, an artificial dry model was produced by drying OBS. Figure 6a shows the mean annual precipitation of the model for the historical climate (much drier than observations), and Fig. 6b shows the mean annual precipitation of the model for a future period which is even drier. Figure 6c–f show the CCS error of the bias-adjustment methods according to Eq. (9).

As before, SDM underestimates the CCS (Fig. 6c), while QDM (without the CCS correction) and QM overestimate the CCS (Fig. 6d and e). However, the mean absolute error of QDM (1.9 %) is smaller than those of SDM (4.3 %) and QM (3.3 %). In Fig. 6f with PresRATe, the CCS of the annual precipitation is forced to match the raw model CCS via Eq. (10), therefore, the error is almost 0 %.

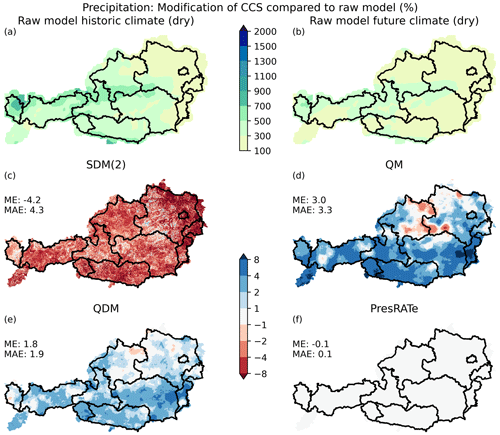
Figure 6 Error of CCS compared to CCS of raw model (Eq. 9). (a) Raw model annual precipitation in historic period (mm). (b) Raw model annual precipitation in future period (mm). (c) SDM, (d) QM, (e) QDM of the CCS and (f) PresRATe. A perfect bias adjustment equals 0 %.

4.3 Demand (3): wet day frequency in dry models

As already discussed in relation to Fig. 4, parametric methods do not always reproduce the observational climate. Furthermore, very few bias-adjustment methods accurately bias correct climate models with a distinct dry bias. We compare SDM, QM and QDM/PresRATe using the artificial dry model data (Fig. 7b). The difference of the model data corrected with SDM(2) minus OBS shows quite good results, but overall the corrected data show a slight wet bias that exceeds 40 mm in some grid cells (Fig. 7c). The area mean annual bias of SDM(2) is 6 mm. QM corrects the precipitation for already existing wet days but cannot add wet days. Thus, there is still a dry bias after bias adjustment (Fig. 7d), where the area mean is −48.5 mm. QDM shows a similar pattern (Fig. 7e) when the algorithm for wet days is not used, hence the name QDMd (Sect. 3.4). QDMd it is almost identical to QM in the historical period, with the only difference that we used 100 discrete percentiles for QDMd and all values for QM for the CDFs. QDM/PresRATe are able of reasonably reproduce climatological precipitation sums in the historical period with an average annual precipitation bias of only 8.6 mm.

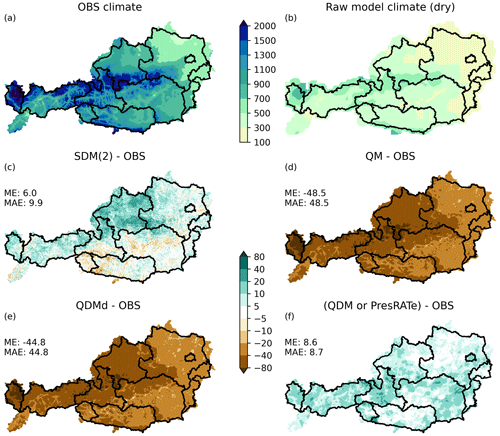
Figure 7 Climatological annual precipitation (mm) sum in the historical period for dry model data. (a) OBS annual precipitation. (b) Raw model (dry) annual precipitation. (c–f) Difference in annual precipitation (model minus observed data) in millimeters for (c) SDM, (d) QM, (e) QDMd (QDM without wet day algorithm) and (f) QDM/PresRATe.

Figure 8 shows the number of precipitation days. The average number of precipitation days per year is much higher in the observations (Fig. 8a) than in the model (Fig. 8b). The difference of Fig. 8a and b is the error of precipitation days per year of the raw model.

The parametric SDM(2) produces too many new precipitation days (Fig. 8c). The average annual wet day bias is +15.5 d. Both the non-parametric QM and QDMd (Fig. 8d and e) cannot change the number of wet days without further modifications, so the average annual wet day bias of −69.9 d of the raw model is unchanged. QDM/PresRATe (Fig. 8f) performs best of all methods with an average bias of only −5 wet days per year. Only very few grid cells exceed a wet day bias of +10 or −10 d.

Figure 8 Wet days per year (≥0.1 mm) in the historical period for dry model data. (a) Annual wet days in OBS. (b) Raw model annual wet days. (c–f) Difference in annual wet days (model minus observed data) for (c) SDM, (d) QM, (e) QDMd and (f) QDM/PresRATe.

5 Discussion and conclusion

Statistical bias-adjustment methods are widely used to improve direct model output from climate models but cannot fully remove all model errors. The adjusted data are often used as input for climate impact studies where biases can significantly alter the impact analysis, so one has to be aware of the limitations of the bias-adjustment methods. We compared different methods (Empirical QM, SDM and QDM/PresRATe) that all adjust the statistical distribution of meteorological variables. We evaluate the methods with the three demands formulated in the introduction for synthetic climate data to show that errors can originate from the bias-adjustment method and not only from climate models.

Table 2 summarizes our main results on two of the three demands. The tested bias-adjustment methods are grouped by how the CDFs are calculated (empirical or parametric) and by whether the bias is assumed to stay constant at quantiles or at a specific value of a variable (trend preserving or trend altering). Seen from another side, some methods determine the quantile for a given future value from the calibration period (trend altering), some directly from the future period (trend preserving). We assume that SDM can be seen as a representative of parametric methods in general because the errors introduced with SDM are mainly due to the fitting of functions.

• Demand (1): QDM/PresRATe and QM are capable of statistically correcting the model's past climate to fit the observations accurately. This is mostly due to the fact that they are non-parametric methods, i.e., they use empirical distribution functions instead of fitted functions (for variables like temperature, precipitation etc.) which allows the CDF to follow any possible shape (Table 2). The fitting of functions (SDM) will always produce errors which can be minimized with a good fitting algorithm (Fig. 4). Also, parametric approaches require knowledge about the statistical distribution of a meteorological variable in order to choose a suitable distribution function.

• Demand (2): QDM/PresRATe and SDM barely enhance or suppress the mean CCS in contrast to traditional QM; i.e., they explicitly reproduce the same CCS as in the raw model. For additive QDM and SDM (e.g., for temperature), this is valid without any limitation (Fig. 5). For multiplicative QDM/PresRATe and SDM (e.g., for precipitation), the CCS is defined as a ratio between historical and future climatological mean. SDM and QDM preserve this ratio at every quantile (Table 2). However, in general, the relative CCSs of monthly and annual means differ from the ratios at quantiles. Depending on the application, a decision has to be made either to conserve the relative CCS at quantiles or at means. In the latter case, an algorithm in PresRATe corrects means to match the raw model's CCS.

• Demand (3): QM is not able to correct models with too few wet days, if applied multiplicatively. SDM(0), SDM(1) and SDM(2) interpolate the wet days to the expected number of wet days which should correct the bias. Figure 8c shows that there is still a wet day bias after correction with SDM(2), though with a positive sign (too many wet days). The reason for this positive wet bias is still in discussion. We suspect that it might be caused by the fitting of gamma functions to the CDFs which introduces new errors. As a solution, QDM and PresRATe include an algorithm that adds additional wet days in order to reproduce the observation's precipitation sums and wet day frequency (Figs. 7f and 8f) by setting the zero-precipitation days to a small non-zero value below a threshold (e.g., 0.05 mm). As a supplementary method, this algorithm can be applied after any bias-adjustment method and could therefore also be applied with QM. In the case of a model having too many wet days, the wet day frequency is automatically corrected with all three methods.

Table 2 As in Table 1. (1), (2) and (3) refer to the demands formulated in the introduction.

A good performance of the corrected data in any of the three demands is crucial, as it is used as input for further impact studies. Impact models (e.g., plant growth models) are often calibrated with bias-corrected historical meteorological data from a climate model. The focus of impact studies often lies on the CCS. If an impact model is calibrated with inaccurate meteorological data in the historical period, the impact of climate change can lead to wrong conclusions even if the CCS is accurate.

To sum up, QDM and PresRATe are able to reproduce the observation's statistical distribution, are able to preserve the raw model's CCS and can add wet days if necessary because of a supplementary algorithm.

QDM along with many other methods corrects each grid cell independently and therefore belongs to the group of univariate bias-adjustment algorithms. We showed that the spatial patterns of the corrected data match the observations for long-term means, which is a significant improvement over the raw model data. However, for spatial patterns of smaller timescales (e.g., a season, a month or a single day), some univariate methods are still able to improve spatial patterns compared to raw model data (Widmann et al., 2019) and the temporal variability of model data (Maraun et al., 2019) to some extent. Other authors find the results of univariate methods for spatial precipitation patterns on specific days in the model unsatisfactory (Pastén-Zapata et al., 2020; Potter et al., 2020; Charles et al., 2020). For a more accurate representation of temporal or spatial correlations, other methods have to be applied (e.g., Pierce et al., 2015; Nguyen et al., 2016, 2017; Mehrotra and Sharma, 2016; Mehrotra et al., 2018; Mehrotra and Sharma, 2019; Volosciuk et al., 2017; Cannon, 2018). However, multivariate methods suffer from disadvantages such as very high computational demands or a limited measure of the full multivariate dependence of structure (e.g., Cannon, 2018; Bürger et al., 2011).

Some authors introduce methods to correct the temporal autocorrelation across several days, weeks or months (Nguyen et al., 2016, 2017; Pierce et al., 2015; Mehrotra and Sharma, 2016). When several timescales are corrected one after the other, this is referred to as nesting approach. A different approach to improve temporal statistics was introduced by Volosciuk et al. (2017) with a two-step approach. It consists of QM on the model's spatial resolution in a first step and a downscaling with a stochastic regression-based model as a second step which adds random small-scale variability. However, the added skill is different from case to case and may even increase the bias at times.

Other authors find the results of univariate methods for spatial precipitation patterns on specific days in the model unsatisfactory (Pastén-Zapata et al., 2020; Potter et al., 2020; Charles et al., 2020). Spatiotemporal statistics like the plausibility of weather patterns can be improved by correcting across multiple timescales and variables (even though on a single grid cell) as shown by Mehrotra and Sharma (2016), Mehrotra et al. (2018) and Mehrotra and Sharma (2019). However, multivariate methods suffer from disadvantages such as very high computational demands or a limited measure of the full multivariate dependence of structure (e.g., Cannon, 2018; Bürger et al., 2011).